To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Geometria wykreślna
Wykład 7
Obrót punktu wokół prostej
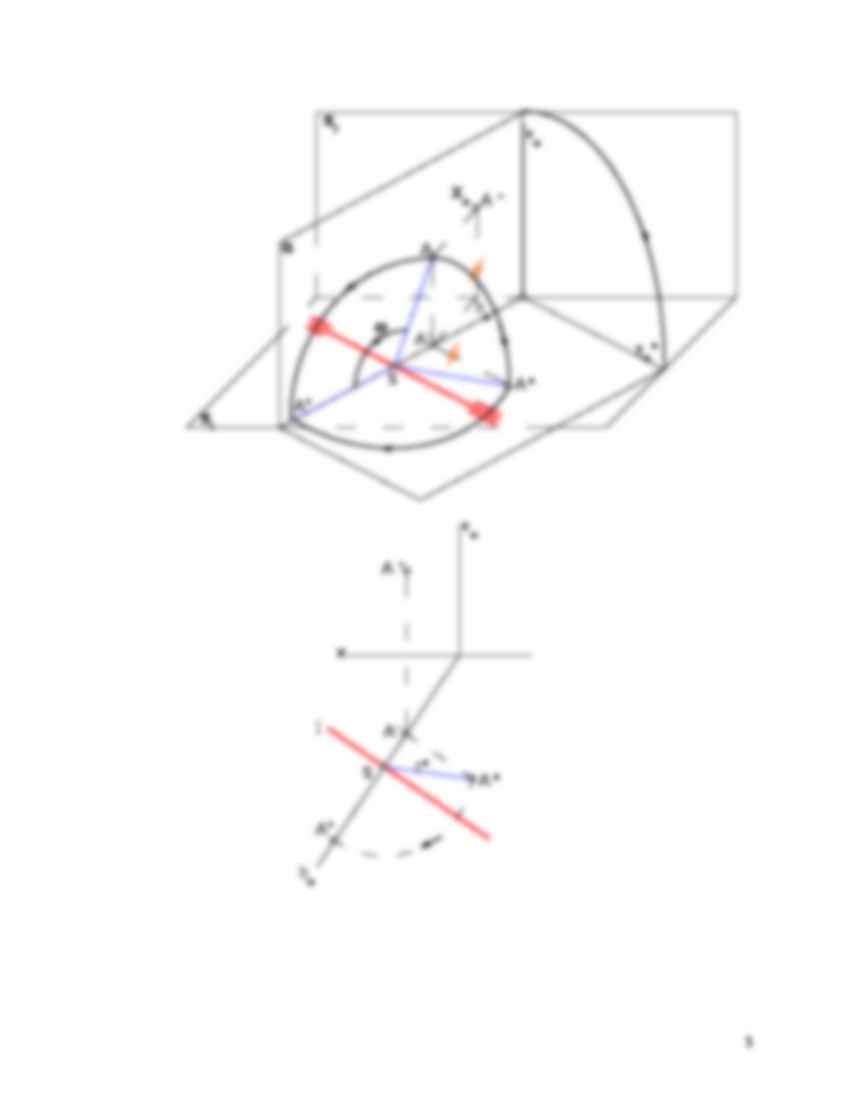
Obrotem punktu A wokół prostej l nazywamy przejście punktu A do nowego położenia Ao po łuku o promieniu równym odległości S.A., który leży na płaszczyźnie prostopadłej do prostej l. Prostą l nazywamy osią obrotu, płaszczyznę płaszczyzną obrotu, punkt S środkiem obrotu, a odległość AS promieniem obrotu. Rzeczywista długość odcinka wyznaczona metodą obrotu
Rzeczywista wielkość trójkąta wyznaczona metodą obrotu
Kład punktu
Kład punktu A wokół prostej l leżącej na którejś z rzutni nazywamy takie przekształcenie w którym punkt obracany jest na płaszczyźnie prostopadłej do prostej l o taki kąt aby po obrocie znalazł się na rzutni.
Kolejność postępowania:
Przez punkt A prowadzimy płaszczyznę prostopadła do niej. Płaszczyznę tę nazywamy płaszczyzną obrotu.
Punkt przecięcia S płaszczyzny i prostej l jest środkiem obrotu.
Dokonujemy kładu płaszczyzny na rzutnię 1. Odległość punktu S od kładu punktu A* jest promieniem obrotu.
Obracamy punkt A* o taki kąt aby znalazł się on na śladzie h Rzeczywista odległość między dwiema prostymi równoległymi
Zadania:
Wyznaczyć rzeczywistą długość odcinka AB metodą obrotu.
Wyznaczyć rzeczywistą wielkość trójkąta ABC leżącego na płaszczyźnie pionowo-rzutującej metodą obrotu.
Dane są rzuty trójkąta ABC leżącego na płaszczyźnie dowolnej. Wyznaczyć metodą obrotu kąt nachylenia tego trójkąta do rzutni poziomej oraz rzeczywistą wielkość tego trójkąta. (zad 1 ark3)
Wyznacz rzeczywistą odległość między dwiema prostymi równoległymi metodą kładu.
Wyznacz rzeczywistą odległość punktu P od prostej m metodą kładu.
Wyznacz rzeczywisty kąt między dwiema prostymi przecinającymi się metodą kładu(zad 2 ark3). 5
Hn' Hn” Hm' Hm” n ”
... zobacz całą notatkę






Komentarze użytkowników (0)