Wykład - energia potencjalna

Nasza ocena:

3
Pobrań: 14
Wyświetleń: 763
Komentarze: 0
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
Wykład - energia potencjalna - strona 1 Wykład - energia potencjalna - strona 2 Wykład - energia potencjalna - strona 3

Fragment notatki:

Energia potencjalna
Pole elektryczne jest polem zachowawczym – praca w tym polu nie zalezy od
drogi, a tylko od położenia początkowego i końcowego.
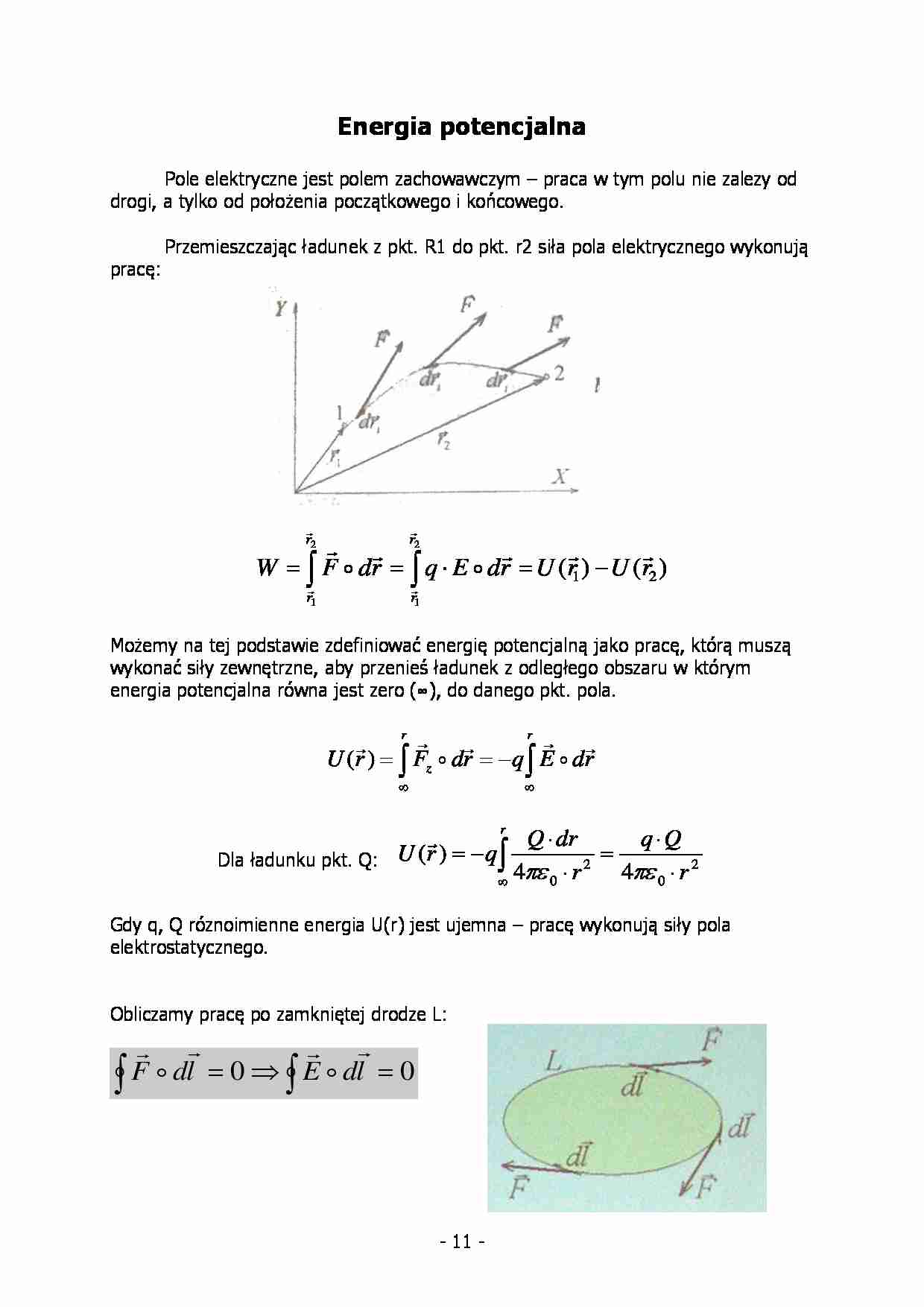
Przemieszczając ładunek z pkt. R1 do pkt. r2 siła pola elektrycznego wykonują
pracę:

r2


r1

r1
  r2



W   F  dr   q  E  dr  U (r1 )  U (r2 )
Możemy na tej podstawie zdefiniować energię potencjalną jako pracę, którą muszą
wykonać siły zewnętrzne, aby przenieś ładunek z odległego obszaru w którym
energia potencjalna równa jest zero (∞), do danego pkt. pola.
r 
r 



U (r )   Fz  dr  q  E  dr



Q  dr
q Q
U (r )  q 

2
4 0  r
4 0  r 2

r
Dla ładunku pkt. Q:
Gdy q, Q róznoimienne energia U(r) jest ujemna – pracę wykonują siły pola
elektrostatycznego.
Obliczamy pracę po zamkniętej drodze L:
 
 
 F  dl  0   E  dl  0
- 11 -
Pole wektorowe spełniające taką właściwość nosi nazwę pola bezwirowego – pole
elektrostatyczne jest polem bezwirowym.
Potencjał pola elektrostatycznego
Stosunek energii potencjalnej ładunku q do wartości do wartości tego ładunku
nazywany jest potencjałem pola elektrostatycznego.

 U (r ) 
J
V (r ) 
 V  
q
C



W  q  V (r1 )  V (r2 )
Dla ładunku pkt. Q:

V (r ) 
Q
4 0  r
Dla układu ładunków pkt.:

V (r )  
i
qi
 
4 0  r1  r2
Związek pomiędzy potencjałem a natężeniem pola elektrycznego:
r 



U (r )  q  E  dr  q V (r )

r 


 V (r )    E  dr

Różnica potencjałów pomiędzy pkt. 1 i 2 wynosi zatem:
r2
r2
   r1   
 


V (r2 )  V (r1 )    E  dr     E  dr     E  dr




 

- 12 -
Dla pola jednorodnego:
r2
 


V  V (r2 )  V (r1 )    E  dr


 
V   E  (r2  r1 )  E  r
Pole elektryczne skierowane jest w stronę niższego potencjału.
Przykład (1) Obliczmy różnicę potencjałów dka dwuch płyt o powierzchni s,
znajdujących się w odległości d od siebie, naładowanych przeciwnie ładunkami Q.

Q
S
 
Q
E  
0 0  S

Qd
V  E  d 
0  S
Przykład (2) Kabel koncentryczny (współosiowy) składa się z drutu o promieniu r1
otoczonego wydrążonym przewodnikiem walcowym o promienu r2. Liniowe gęstości
ładunku na tych przewodnikach są ruwne n i –n. Znaleźć różnicę potencjałów między
tymi dwoma przewodnikami
Ponieważ pole ma kierunek radialny:
r2
V   E  dr
r1
Podstawiając wynik z omówionego przykładu:
r


dr

V  
dr 

ln 2
2 0 r
2 0  r 2 0 r1
r
r
r2
r2
1
1
- 13 -
Powierzchnia stałego potencjału
Powierzchnia stałego potencjału wyznacza równanie:

V (r )  const

dV  0

 

E  dr  0 E  dr

Warunek ten oznacza, ze wektor pola jest w każdym punkcie prostopadły do
powierzchni stałego potencjału.
Związek potencjału z natężeniem pola
Mamy:

r2
 
 
V    E  dr  dV   E  dr

r1
Rozpisując te wyrażenie dla składowych pola:
dV 
 
V
V
V
dx 
dy 
dz E  dr  Ex  dx  E y  dy  Ez  dz
x
y
z
Porównując stronami otrzymujemy:
Ex 
V
V
V
;E y 
; Ez  ... zobacz całą notatkę



Komentarze użytkowników (0)

Zaloguj się, aby dodać komentarz