Wózek; warunki dla kół

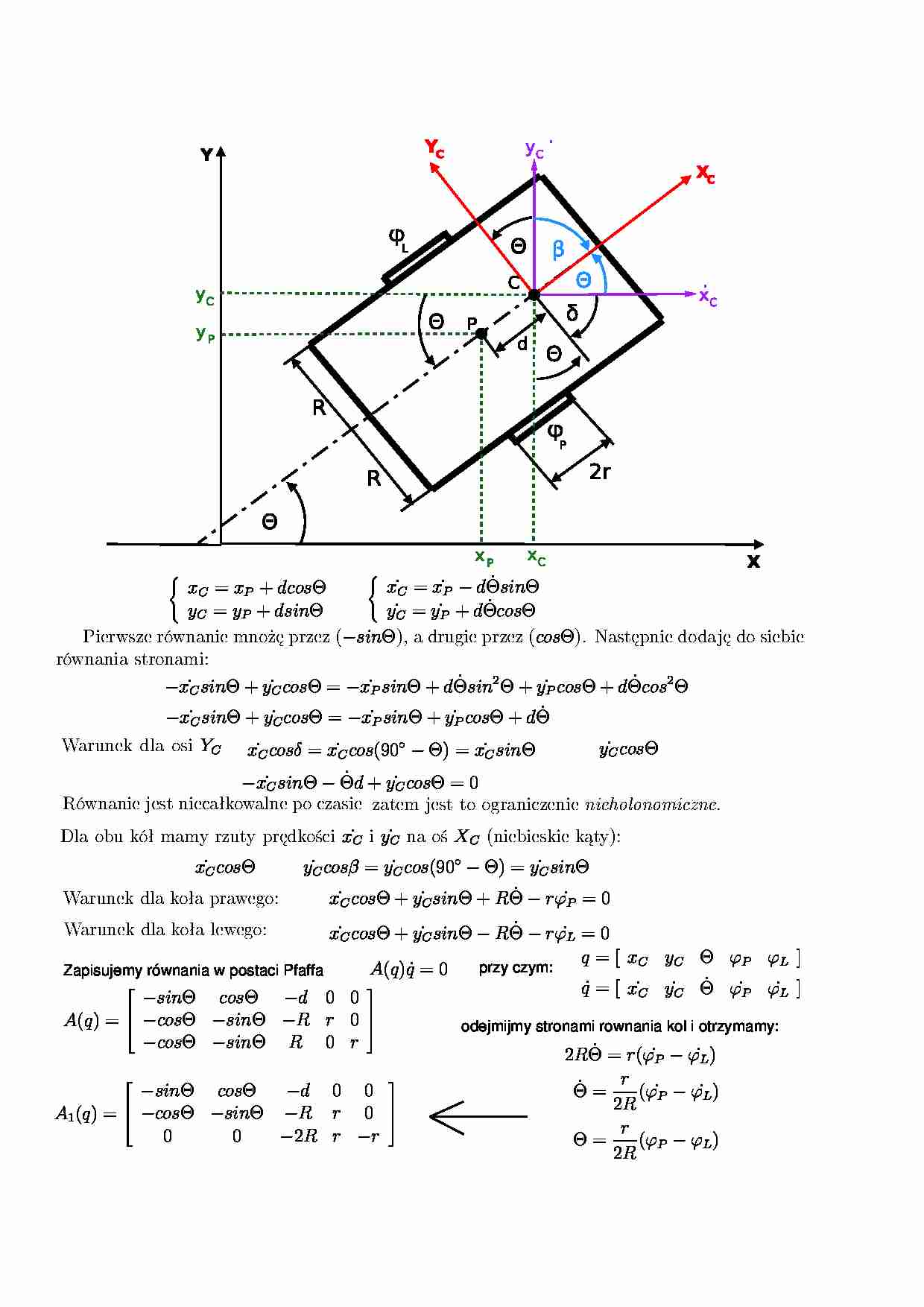
ž(”„"‹Ø‚G„(g‰·eˆˆ“šl‡”“|yŠD(ž"„(|}ŠI„ªÙ Ú³ÛyÜ ÝÊÞDÝÊÙßÝÊà—Ú³áeâ(ÙßÛh en­®¡| |}ŠD„¥‚G„(gGÓ|yŠD„((BÇF~ˆ®¡µ“¤I|}„µ–’ˆ¥(ž(“geŠI„ xC = xP + dcosΘ yC = yP + dsinΘ ˙ xC = ˙ xP − d ˙ ΘsinΘ ˙ yC = ˙ yP + d ˙ ΘcosΘ zrŠD„(‡‰¡gež"„n‡G­®¡| “|}ŠI„%‹œ|}ˆ“£(´%–}‡Gž(„(ž1Ÿ −sinΘ §W•x£‰}‡G{}šlŠI„µ–}‡ež"„(žŸ cosΘ §h¥¶·“gGe´(–}|yŠD„%‰}ˆB‰ s‚G´%‰}ˆ£gGŠD„"‘}ŠD„ ‡e­®¡| |}Š‘—gGe‡eˆl|}“‹œŠ¸k − ˙ xC sinΘ + ˙ yCcosΘ = − ˙ xP sinΘ + d ˙ Θsin2Θ + ˙ yP cosΘ + d ˙ Θcos2Θ − ˙ xC sinΘ + ˙ yCcosΘ = − ˙ xP sinΘ + ˙ yP cosΘ + d ˙ Θ Á“‡e{}|y„(~‰}¤‘§ˆlgeŠ YC ˙ xCcosδ = ˙ xC cos (90◦ − Θ) = ˙ xC sin Θ ˙ yCcos Θ − ˙ xC sinΘ − ˙ Θd + ˙ yCcosΘ = 0 æp¤Dˆ“‘}{§~“­xÇ)‹œ“‹†fćGž({ydf§–y‡e´(‰y~“ˆl…G(Š ˙ xC Š ˙ yC | —ˆl… XC Ÿa|yŠD„(‘yŠD„(gG~“ŠD„£~ÊÏdfy§k ˙ xC cos Θ ˙ yCcosβ = ˙ yCcos (90◦ − Θ) = ˙ yCsin Θ Á“‡A{y|}„~ĉy¤[—~“ˆNÇ.—–}‡”¢¡º„šlˆ}k ˙ xC cosΘ + ˙ yCsinΘ + R ˙ Θ − r ˙ ϕP = 0 Á“‡A{y|}„~ĉy¤[—~“ˆNÇ.—¤,„¡º„š“ˆ}k ˙ xC cosΘ + ˙ yCsinΘ − R ˙ Θ − r ˙ ϕL = 0 Zapisujemy równania w postaci Pfaffa A (q) ˙q = 0 q = [ xC yC Θ ϕP ϕL ] ˙q = [ ˙ xC ˙ yC ˙ Θ ˙ ϕP ˙ ϕL ] A (q) =    −sinΘ cos Θ −d 0 0 −cosΘ −sinΘ −R r 0 −cosΘ −sinΘ R 0 r    2R ˙ Θ = r( ˙ ϕP − ˙ ϕL) ˙ Θ = r 2R ( ˙ ϕP − ˙ ϕL) Θ = r 2R (ϕP − ϕL) A1(q) =    −sinΘ cos Θ −d 0 0 −cosΘ −sinΘ −R r 0 0 0 −2R r −r    przy czym: odejmijmy stronami rownania kol i otrzymamy: ... zobacz całą notatkę