To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
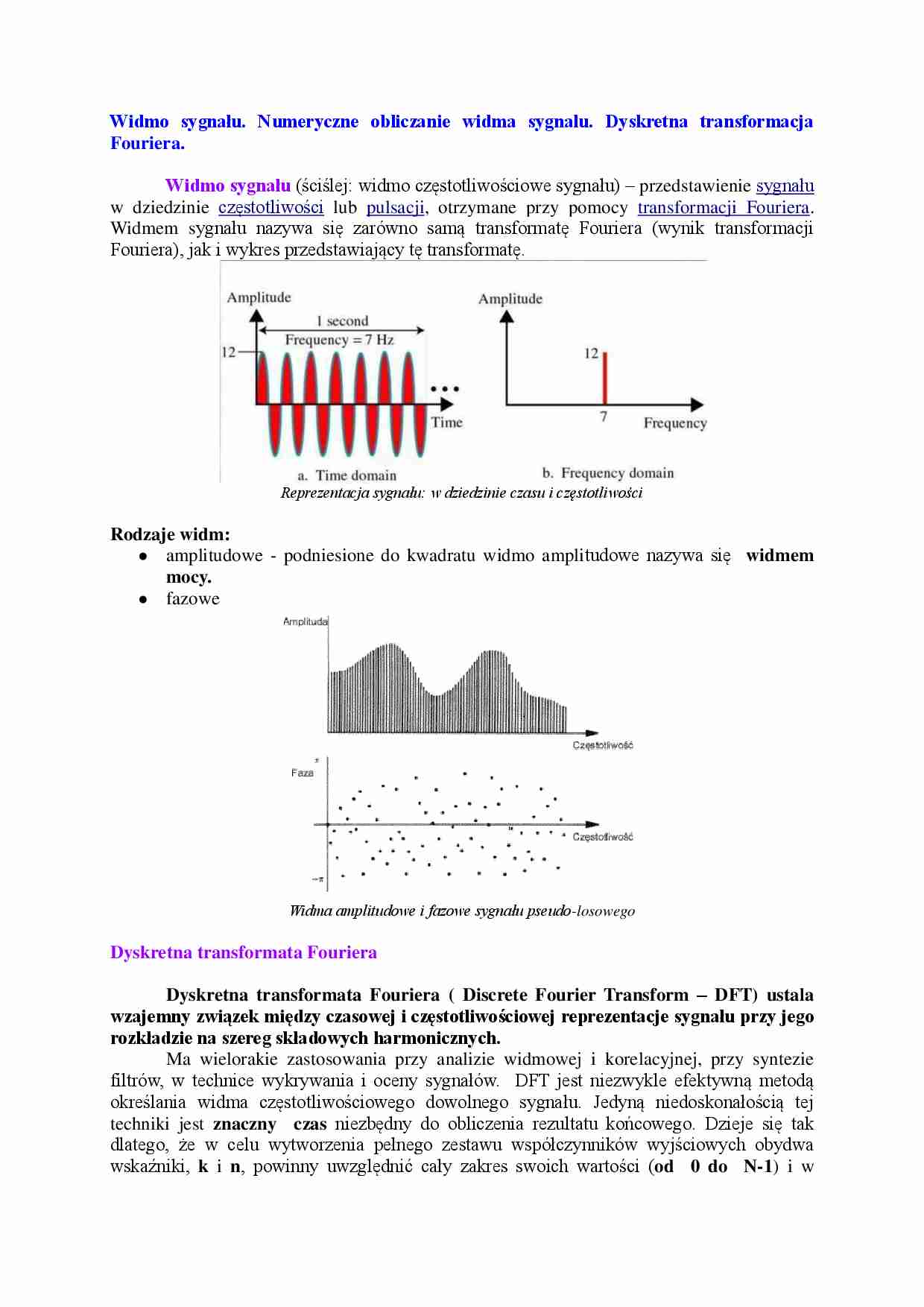


Widmo sygnału. Numeryczne obliczanie widma sygnalu. Dyskretna transformacja Fouriera. Widmo sygnału (ściślej: widmo częstotliwościowe sygnału) - przedstawienie sygnału w dziedzinie częstotliwości lub pulsacji, otrzymane przy pomocy transformacji Fouriera. Widmem sygnału nazywa się zarówno samą transformatę Fouriera (wynik transformacji Fouriera), jak i wykres przedstawiający tę transformatę.
Reprezentacja sygnału: w dziedzinie czasu i częstotliwości
Rodzaje widm:
amplitudowe - podniesione do kwadratu widmo amplitudowe nazywa się widmem mocy.
fazowe
Widma amplitudowe i fazowe sygnału pseudo-losowego
Dyskretna transformata Fouriera Dyskretna transformata Fouriera ( Discrete Fourier Transform - DFT) ustala wzajemny związek między czasowej i częstotliwościowej reprezentacje sygnału przy jego rozkładzie na szereg składowych harmonicznych. Ma wielorakie zastosowania przy analizie widmowej i korelacyjnej, przy syntezie filtrów, w technice wykrywania i oceny sygnałów. DFT jest niezwykle efektywną metodą określania widma częstotliwościowego dowolnego sygnału. Jedyną niedoskonałością tej techniki jest znaczny czas niezbędny do obliczenia rezultatu końcowego. Dzieje się tak dlatego, że w celu wytworzenia pełnego zestawu współczynników wyjściowych obydwa wskaźniki, k i n, powinny uwzględnić cały zakres swoich wartości (od 0 do N-1) i w związku z tym powinno być wykonane N2 obliczeń.
Dyskretna i odwrotna transformata Fouriera:
Sekwencja {xn} reprezentuje sobą próbki sygnału, zaś sekwencja {ck}- współczynniki widmowe.
W dyskretnej transformacie Fouriera wykorzystuje się system funkcji wykładniczych (angl. discrete exponential functions - DEF) zdefiniowanych za pomocą następującego wzoru:
Wielkość w k,n zwykle nazywa się współczynnikiem skrętu i reprezentuje sobą wektor w płaszczyźnie zespolonej. Cały system DEFmożna zapisać w postaci macierzy EN, której wiersze są numerowane za pomocą indeksu k, kolumny - za pomocą indeksu n, a na skrzyżowaniu k-tego wiersza i n-tej kolumny zapisana jest wartość w k,n. W DFT ta sama wartość wN występuje w obliczeniach wielokrotnie, gdyż jest ona funkcją okresową o limitowanej liczbie odrębnych wartości. Zadaniem więc szybkiego przekształcenia Fouriera (FFT), i jego odwrotności (IFFT), jest wykorzystanie tej nadmiarowości w celu redukcji liczby niezbędnych obliczeń cząstkowych. Z tego powodu istotne znaczenie mają procedury obliczeniowe redukujące liczbę mnożeń i sumowań. Jedną z takich procedur jest algorytm szybkiej transformaty Fouriera (FFT).
(…)
… będą liczbami zespolonymi, wtedy dyskretna transformata Fouriera jest określona wzorem:
Najpopularniejszą wersją FFT jest FFT o podstawie 2. Jest to bardzo efektywna operacja, jednak wektor próbek wejściowych (spróbkowany sygnał) musi mieć długość , gdzie to pewna liczba naturalna. Wynik otrzymuje się na drodze schematycznych przekształceń,. Podstawową „cegiełką” algorytmu FFT jest operacja motylkowa:
Złożoność obliczeniowa FFT wynosi , zamiast algorytmu wynikającego wprost ze wzoru określającego dyskretną transformatę Fouriera. Dzięki istnieniu takiego algorytmu praktycznie możliwe stało się cyfrowe przetwarzanie sygnałów (DSP), a także zastosowanie dyskretnych transformat kosinusowych (DCT) (JPEG, MP3 itd.) do kompresji.
Na przykład dla N=4096 bezpośrednie wykorzystanie wzoru dla DFT wymaga 16…
… nieskończonego sumowania, gdyż nigdy nie osiągnęlibyśmy wyniku końcowego.
Po drugie, czas przeznaczony na osiągnięcie wartości wyjściowej jest limitowany.
Wynika stąd, że liczba częstotliwości biorących udział w obliczeniach jest ograniczona. W przypadku sygnału cyfrowego przetwarzanie ma charakter pewnych obliczeń numerycznych.
…
... zobacz całą notatkę






Komentarze użytkowników (0)