To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
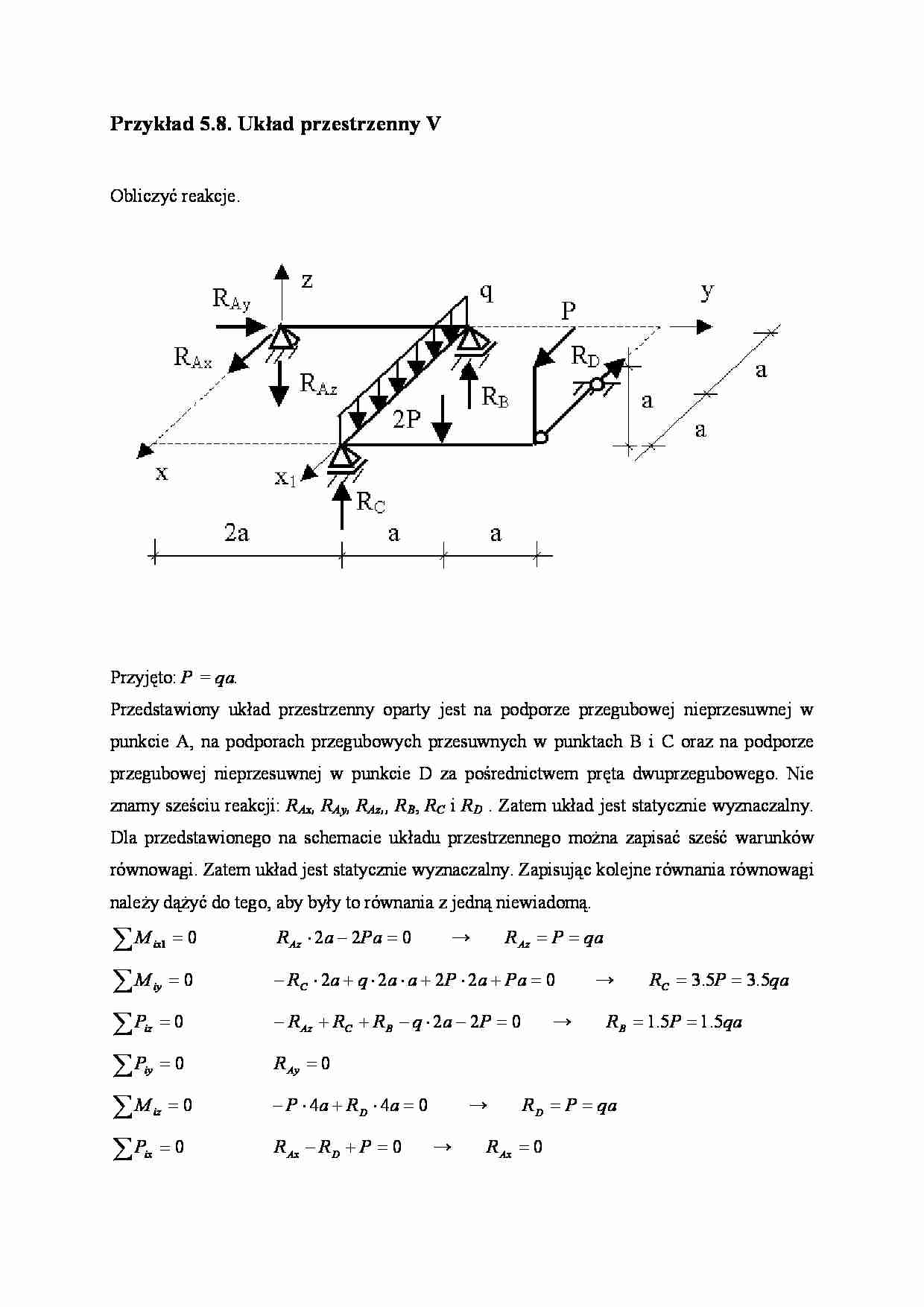

Przykład 5.8. Układ przestrzenny V Obliczyć reakcje. Przyjęto: P = qa. Przedstawiony układ przestrzenny oparty jest na podporze przegubowej nieprzesuwnej w punkcie A, na podporach przegubowych przesuwnych w punktach B i C oraz na podporze przegubowej nieprzesuwnej w punkcie D za pośrednictwem pręta dwuprzegubowego. Nie znamy sześciu reakcji: RAx, RAy, RAz,, RB , RC i RD . Zatem układ jest statycznie wyznaczalny. Dla przedstawionego na schemacie układu przestrzennego można zapisać sześć warunków równowagi. Zatem układ jest statycznie wyznaczalny. Zapisując kolejne równania równowagi należy dążyć do tego, aby były to równania z jedną niewiadomą. 0 1 = ∑ ix M 0 2 2 = − ⋅ Pa a R Az → qa P R Az = = 0 = ∑ iy M 0 2 2 2 2 = + ⋅ + ⋅ ⋅ + ⋅ − Pa a P a a q a R C → qa P R C 5 . 3 5 . 3 = = 0 = ∑ iz P 0 2 2 = − ⋅ − + + − P a q R R R B C Az → qa P R B 5 . 1 5 . 1 = = 0 = ∑ iy P 0 = Ay R 0 = ∑ iz M 0 4 4 = ⋅ + ⋅ − a R a P D → qa P R D = = 0 = ∑ ix P 0 = + − P R R D Ax → 0 = Ax R 2 W celu sprawdzenia poprawności obliczeń korzystamy z warunku równowagi, z którego nie korzystaliśmy poprzednio 0 = ∑ ix M 0 3 2 2 2 2 2 = ⋅ − ⋅ + ⋅ + ⋅ ⋅ − a P a R a R a a q C B → 0 6 7 3 4 2 2 2 2 = − + + − qa qa qa qa
... zobacz całą notatkę




Komentarze użytkowników (0)