To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


5. TWIERDZENIA O FUNKCJACH RÓŻNICZKOWALNYCH 5.1 TWIERDZENIA O WARTOŚCI ŚREDNIEJ Tw. 5.1.1 (Rolle'a) funkcja f jest ciągła na [ a , b ]
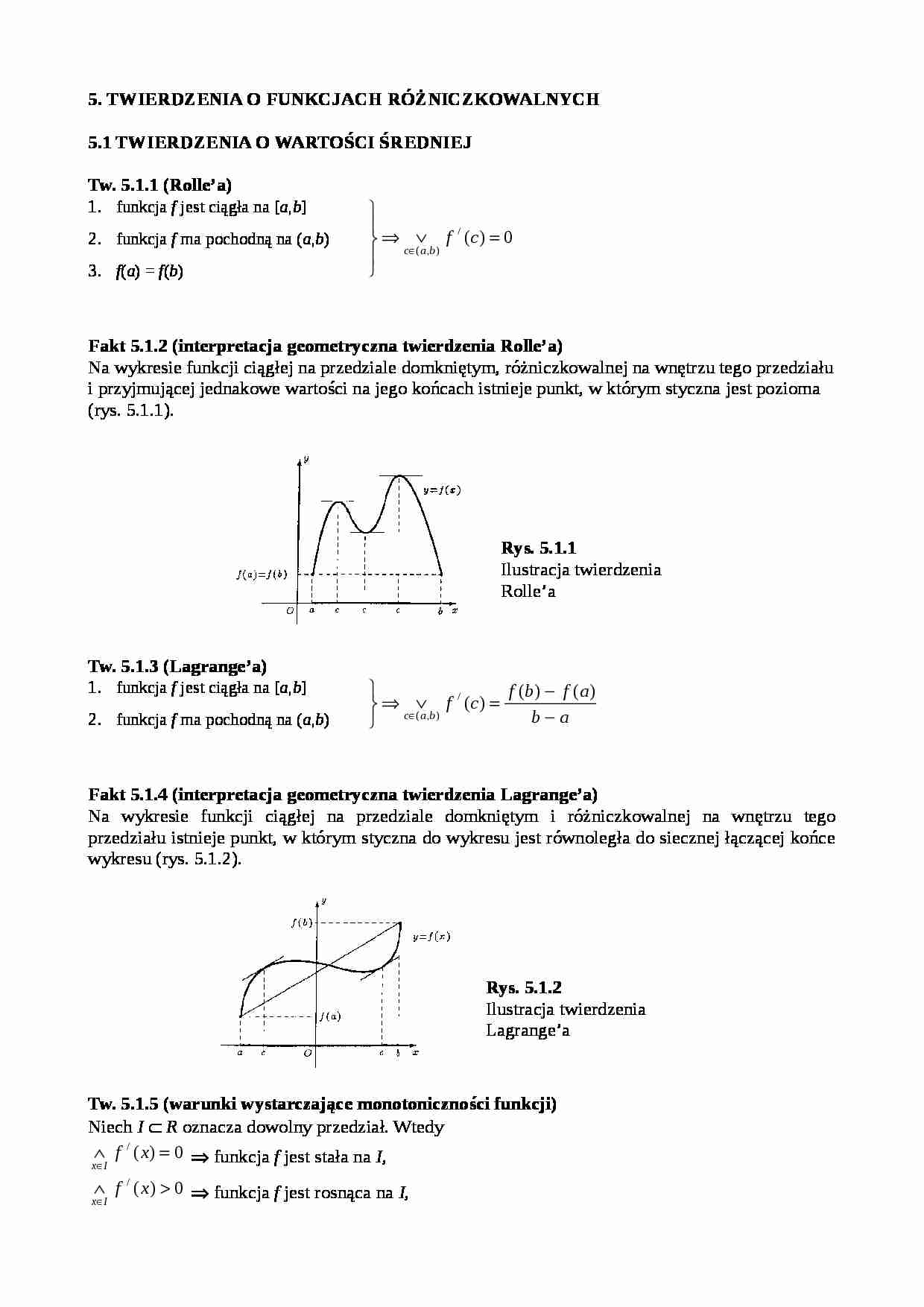
funkcja f ma pochodną na ( a , b ) f ( a ) = f ( b ) Fakt 5.1.2 (interpretacja geometryczna twierdzenia Rolle'a) Na wykresie funkcji ciągłej na przedziale domkniętym, różniczkowalnej na wnętrzu tego przedziału i przyjmującej jednakowe wartości na jego końcach istnieje punkt, w którym styczna jest pozioma (rys. 5.1.1).
Rys. 5.1.1 Ilustracja twierdzenia Rolle'a
Tw. 5.1.3 (Lagrange'a) funkcja f jest ciągła na [ a , b ]
funkcja f ma pochodną na ( a , b )
Fakt 5.1.4 (interpretacja geometryczna twierdzenia Lagrange'a) Na wykresie funkcji ciągłej na przedziale domkniętym i różniczkowalnej na wnętrzu tego przedziału istnieje punkt, w którym styczna do wykresu jest równoległa do siecznej łączącej końce wykresu (rys. 5.1.2).
Rys. 5.1.2 Ilustracja twierdzenia Lagrange'a
Tw. 5.1.5 (warunki wystarczające monotoniczności funkcji) Niech I R oznacza dowolny przedział. Wtedy
funkcja f jest stała na I ,
funkcja f jest rosnąca na I ,
funkcja f jest niemalejąca na I ,
funkcja f jest malejąca na I ,
funkcja f jest nierosnąca na I .
Uwaga . Jeżeli dla każdego x I , przy czym równość zachodzi jedynie dla skończonej liczby punktów z przedziału I , to funkcja f jest rosnąca na I . Podobnie jest dla funkcji malejącej.
Tw. 5.1.6 (o pochodnej funkcji monotonicznej) funkcja f jest rosnąca na I R funkcja f ma pochodną na przedziale I dla każdego x I Uwaga . Prawdziwe są także analogiczne twierdzenia dla pozostałych rodzajów funkcji monotonicznych.
Tw. 5.1.7 (o tożsamościach) Niech funkcje f i g będą określone na przedziale I R oraz niech x 0 I . Wtedy
.
Tw. 5.1.8 (o nierównościach) Niech funkcje f i g będą określone na przedziale I R oraz niech x 0 I . Wtedy
.
Uwaga . Jeżeli jedna z nierówności w założeniach powyższego twierdzenia jest ostra, to nierówność w tezie także jest ostra. Analogiczne twierdzenie prawdziwe jest także dla x
(…)
… ma w punkcie x0 pochodną właściwą k-tego rzędu, k N {0}. Wielomian nazywamy wielomianem Taylora rzędu k Funkcji f w punkcie x0. Jeżeli x0 = 0, to wielomian Pk nazywamy wielomianem Maclaurina.
Uwaga. Wielomian Pk jest jedynym wielomianem stopnia k, który spełnia warunki:
, , …, .
Tw. 5.3.2 (wzór Taylora z resztą Lagrange'a)
Jeżeli
funkcja f ma ciągłą pochodną rzędu n - 1 na przedziale [x0,x],
istnieje właściwa pochodna f(n) na przedziale (x0,x),
to
.
Uwaga. Twierdzenie powyższe jest prawdziwe także dla przedziału [x,x0], wtedy c (x,x0). Równość występującą w tezie twierdzenia nazywamy wzorem Taylora. Wyrażenie
nazywamy n-tą resztą Lagrange'a. Resztę tę można także zapisać w postaci
,
gdzie oraz . Dla wzór Taylora przyjmuje postać
,
gdzie c (0,x) dla x > 0 lub c (x,0) dla x < 0. Równość tę nazywamy wzorem Maclaurina.
Fakt 5.3.3 (wzory Maclaurina dla niektórych funkcji elementarnych)
Funkcja Wzór Maclaurina
Uwaga. W powyższej tabeli punkt pośredni c należy do przedziału (0,x), gdy x > 0 albo do przedziału (x,0), gdy x < 0.
Tw. 5.3.4 (uzasadnienie nierówności za pomocą wzoru Taylora)
Niech funkcja f spełnia założenia twierdzenia Taylora oraz niech Rn(t) ≥ 0 dla każdego t (x0,x…
... zobacz całą notatkę






Komentarze użytkowników (0)