To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


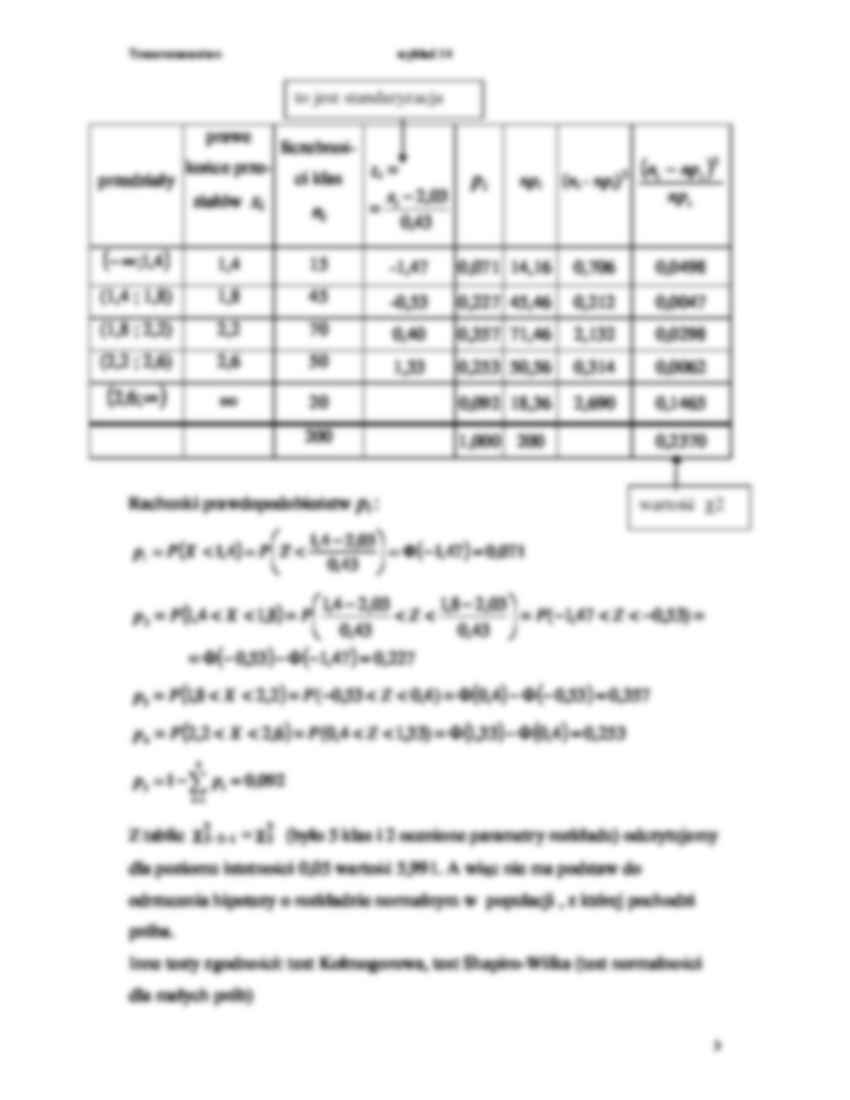
Towaroznawstwo wykład 14 1 Test zgodno ś ci ( χ 2 Pearsona) Testowana hipoteza H0 : zmienna losowa X ma okre ś lony rozkład (np. rozkład normalny, Poissona itp.) Pobieramy n-elementową próbę (n100) , z której budujemy szereg rozdzielczy o r przedziałach klasowych Statystyka testowa : ∑ = − = χ r i i i i np np n 1 2 2 ) ( , gdzie n –ilość obserwacji (liczebność próby) r –ilość klas (przedziałów klasowych) ni –liczebność empiryczna w i -tej klasie pi – prawdopodobieństwo, e zmienna losowa o rozkładzie zdefiniowanym w hipotezie H0 przyjmie wartość z i -tej klasy. Aby policzyć pi nale y najpierw ewentualnie oszacować parametry rozkładu (np. w rozkładzie normalnym µ i σ 2, w rozkładzie Poissona -λ) npi –liczebność teoretyczna w i -tej klasie (średnio tyle obserwacji powinno się znaleźć w i -tej klasie jeśli H0 prawdziwa). Wszystkie npi powinny być równe co najmniej 5, w przeciwnym razie nale y zmniejszyć ilość klas Jeśli hipoteza H0 jest prawdziwa to statystyka χ 2 ma asymptotyczny rozkład χ 2 z r - k -1 stopniami swobody gdzie k – ilość parametrów rozkładu, które musiały być oszacowane na podstawie próby. Towaroznawstwo wykład 14 2 Przebieg testowania hipotezy H0 1. Oszacować parametry rozkładu 2. Obliczyć ilość stopni swobody r-k- 1 i wyznaczyć obszar krytyczny przy ustalonym poziomie istotności α ( ) ∞ χ = α , 2 K 3. Obliczyć p i 4. Obliczyć wartość statystyki ∑ = − = χ r i i i i np np n 1 2 2 ) ( 5. Jeśli χ2∈K to odrzucamy H 0 , czyli rozkład zmiennej losowej X ró ni się istotnie od rozkładu teoretycznego Przykład. Sprawdzić, czy losowa próba przedstawiona w następującym szeregu rozdzielczym pochodzi z populacji o rozkładzie normalnym: przedziały 1-1,4 1,4-1,8 1,8-2,2 2,2-2,6 2,6-3 liczebności klas ni 15 45 70 50 20 Stawiamy hipotezę H0: rozkład jest normalny. Najpierw trzeba oszacować parametry rozkładu normalnego: 43 , 0 ˆ 03 , 2 ˆ ≈ σ ≈ = µ X . Resztę rachunków (wartość funkcji testowej wygodnie jest przeprowadzić w tabelce): 2 α χ 2 1 − − χ k r 1-α α Towaroznawstwo wykład 14 3 przedziały prawe
... zobacz całą notatkę






Komentarze użytkowników (0)