To tylko jedna z 26 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
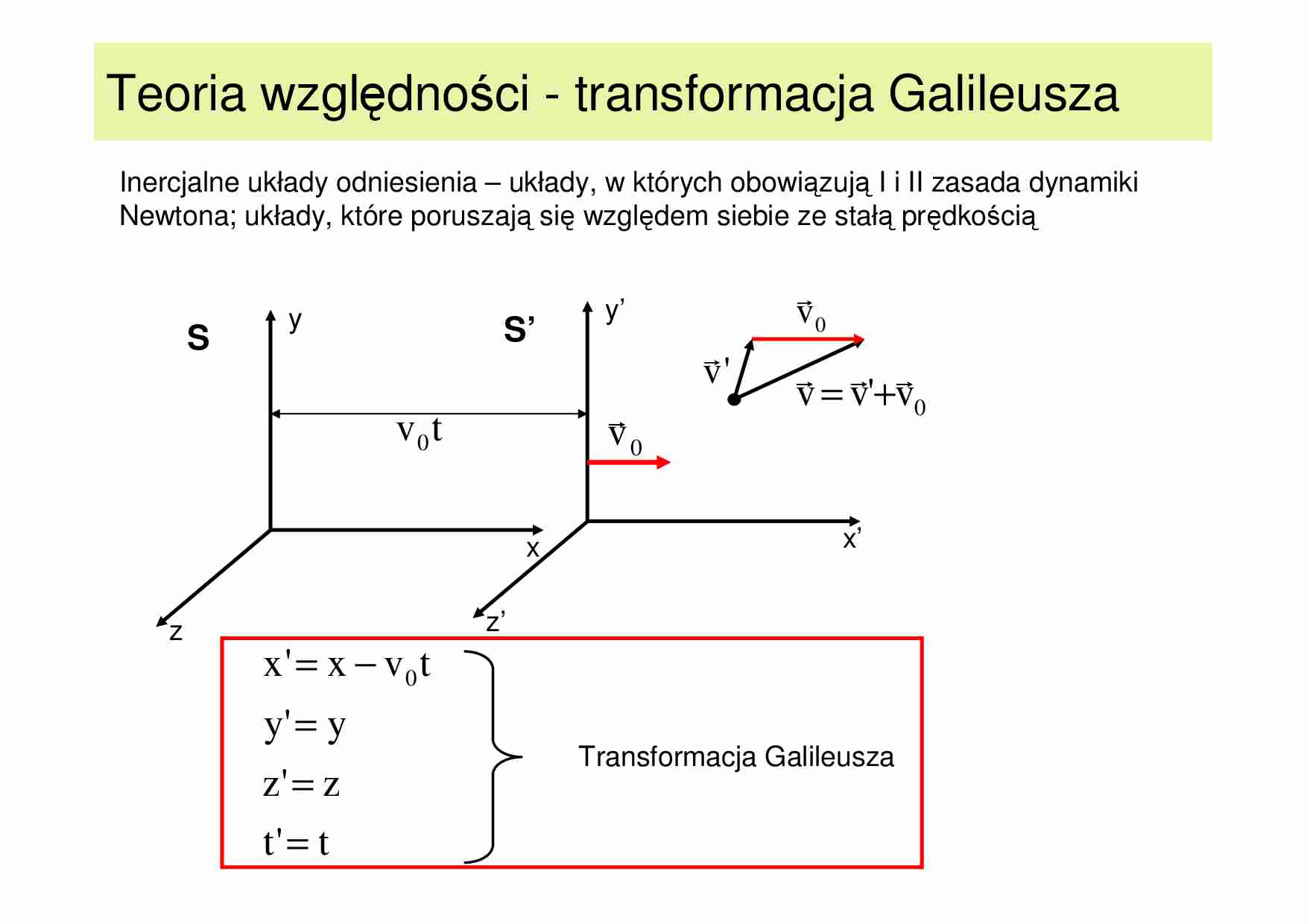


Teoria względności - transformacja Galileusza
Inercjalne układy odniesienia – układy, w których obowiązują I i II zasada dynamiki
Newtona; układy, które poruszają się względem siebie ze stałą prędkością
S
y
S’
x
z
x' = x − v0 t
y' = y
z' = z
t' = t
r
v'
r
v0
v0 t
r
v0
y’
r r r
v = v'+v0
x’
z’
Transformacja Galileusza
Teoria względności - transformacja Galileusza
x' = x − v0 t
x = x '+ v 0 t
y' = y
z' = z
y = y'
z = z'
t = t'
t' = t
d
:
dt
d
:
dt
dx ' dx
=
− v0
dt dt
dy' dy
=
dt dt
dz' dz
=
dt dt
dv'x dv x
=
dt
dt
dv' y dv y
=
dt
dt
dv'z dv z
=
dt
dt
transformacja odwrotna
⇒ v' x = v x − v 0
⇒ v' y = v y
Dodawanie prędkości:
r r r
v' = v − v0
⇒ v'z = v z
r r r
v = v'+v0
⇒ a 'x = a x
⇒ a 'y = a y
⇒ a 'z = a z
r r
a' = a
Przyspieszenie jest
niezmiennikiem transformacji
Galileusza
Teoria względności - transformacja Galileusza
r r
a ' = a /⋅ m
r
r
ma ' = ma
r r
F' = F
Siły w obu układach są jednakowe - niezmienne są prawa mechaniki przy przejściu
z jednego układu inercjalnego do drugiego układu inercjalnego - zasada
względności mechaniki klasycznej (zasada względności Galileusza)
Granice stosowalności mechaniki klasycznej:
1) mechanika relatywistyczna
2) mikroświat - mechanika kwantowa
v→c
Teoria względności
Dodatni ładunek q poruszający się z prędkością v w polu magnetycznym o indukcji B:
S
r
B
z
S’
r
F
q
r
v
r
v
r
v' = 0
r
r r
F = qv × B
x’
q
y
x
y’
z’
r
F=0
Zjawiska elektromagnetyczne nie są niezmiennicze względem transformacji Galileusza
Teoria względności
1887 r – doświadczenie Michelsona i Morleya:
zwierciadło
zwierciadło
półprzepuszczalne
zwierciadło
źródło światła
detektor
- pomiar prędkości światła polegający na porównaniu rozchodzenia się prędkości dwóch wiązek
świetlnych w próŜni, z których jedna poruszała się w kierunku północ - południe, druga w
kierunku wschód - zachód. NaleŜało oczekiwać, Ŝe prędkości tych wiązek będą róŜne na
skutek ruchu orbitalnego Ziemi (30 km/s)
Doświadczenie pokazało, Ŝe w próŜni światło porusza się z prędkością c, niezaleŜnie od
ruchu źródła lub obserwatora, czyli niezaleŜnie od wyboru układu odniesienia
Teoria względności – jednoczesność zdarzeń
Obserwator znajduje się na platformie poruszającej się
z prędkością v
t’=0
Światło dociera jednocześnie do ścianek
- zdarzenia jednoczesne
t’
Obserwator znajduje się obok platformy
t=0
t
Wg transformacji Galileusza światło powinno
docierać do ścianek w róŜnych chwilach
czasu - zdarzenia niejednoczesne
Wniosek: załoŜenie, Ŝe t = t’ jest błędne - nie istnieje czas absolutny
niezaleŜny od układu odniesienia
Szczególna teoria względności
1905 r – A. Einstein – szczególna teoria względności – teoria relatywistyczna
POSTULATY:
1. Wszystkie zjawiska przebiegają jednakowo we wszystkich układach
inercjalnych. Wszystkie układy inercjalne są fizycznie równowaŜne – zasada
względności
2. We wszystkich inercjalnych układach odniesienia wartość prędkości światła w
próŜni jest jednakowa i wynosi c
c = (2.99792458
(…)
… spoczynkowej = 0
m=0
E 2 − p 2c2 = m 2c4
E 2 = p 2c 2
⇒ E = pc
r E r
p= 2 v ⇒ v=c
c
poruszają się z prędkością c
np. foton - kwant energii światła
E = hν
Energia fotonu:
Foton ma zerową masę spoczynkową, warunkiem istnienia fotonu jest energia i pęd. Dzięki
równowaŜności masy i energii moŜna mu przypisać masę relatywistyczną:
hν
E = m f c = hν ⇒ m f = 2
c
2
Masa relatywistyczna oddziałuje grawitacyjnie…
…
p3 =
mv z
v2
1− 2
c
m(v ) =
p4 =
mc
v2
1− 2
c
m
1−
2
v
c2
masa
relatywistyczna
Teoria względności
Masa relatywistyczna:
m(v)
m(v ) =
m0
v2
1− 2
c
m0 – masa spoczynkowa
m0
0.0
0.2
0.4
0.6
0.8
1.0
v/c
ze wzrostem prędkości wzrasta takŜe masa,
przy czym dla
v → c, m(v ) → ∞
JeŜeli m0 ≠0 to prędkość ciała v < c – nie moŜe być = c;
jeŜeli v<<c to m(v) = m0.
Teoria względności
II zasada dynamiki:
JeŜeli m…
... zobacz całą notatkę






Komentarze użytkowników (0)