To tylko jedna z 18 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


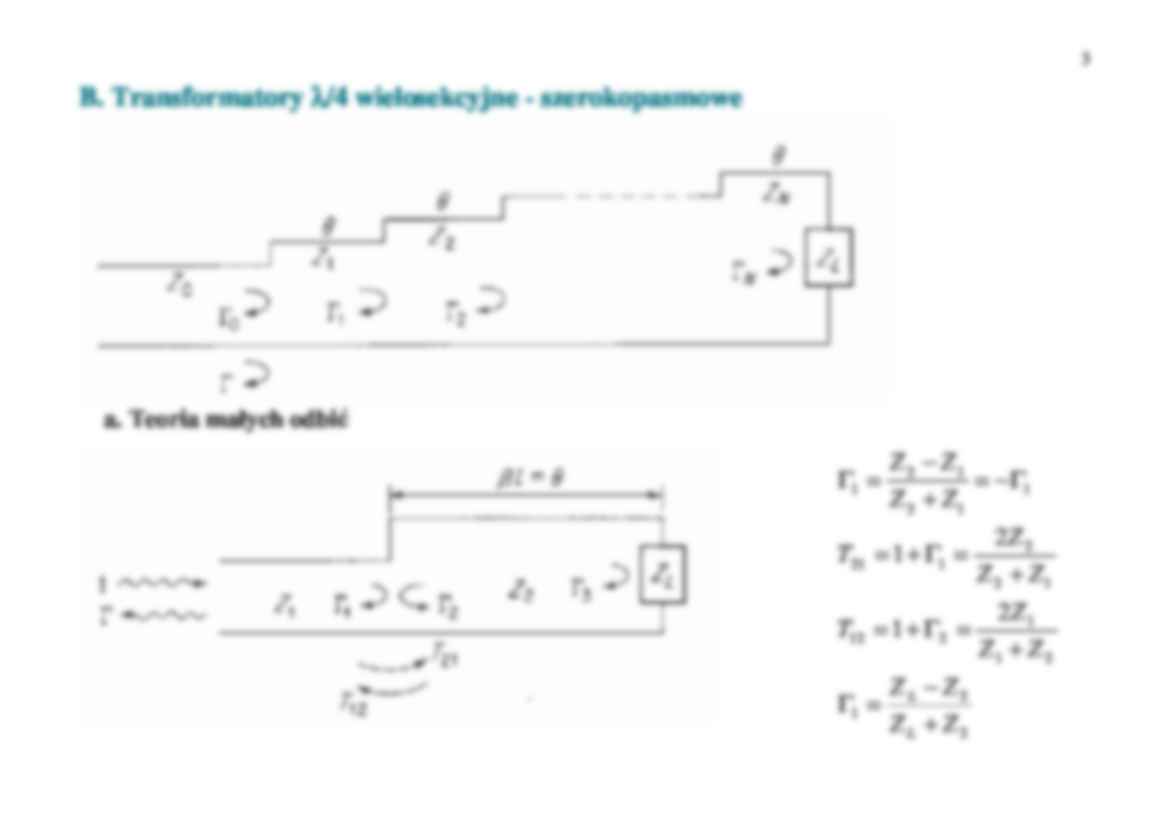
Transformatory λ/4 i o zbie nym przej ciu– dopasowuj ce: • dwie linie transmisyjne o ró nych impedancjach charakterystycznych • falowód metalowy pusty i wypełniony jednorodnym dielektrykiem lub w pewnym tylko obszarze • dwa falowody o ró nych wymiarach geometrycznych (szeroko ci lub/i wysoko ci) A. Transformator λ /4 pojedynczy - w skopasmowy Przy cz stotliwo ci rodkowej fo, przy której na długo ci transformatora odkłada si ¼ długo ci fali, kiedy Θ = βl = π/2 1 2 2 Z Z Z Z L in ≡ = TECHNIKA B.W.CZ, 2009 Zin 2 Charakterystyka transformatora pojedynczego 2 1 2 1 2 1 sec 2 1 1 − + = = Γ θ ρ Z Z Z Z L in 2 1 1 1 1 1 ) ( 2 cos m L L m m Z Z Z Z ρ ρ θ − − = − 3 B. Transformatory λ /4 wielosekcyjne - szerokopasmowe a. Teoria małych odbi 2 2 1 2 1 1 2 12 1 2 2 1 21 1 1 2 1 2 1 2 1 2 1 Z Z Z Z Z Z Z T Z Z Z T Z Z Z Z L L + − = Γ + = Γ + = + = Γ + = Γ − = + − = Γ 4 Wielokrotne odbicia fal w obwodzie z dwoma odbijaj cymi zł czami TECHNIKA B.W.CZ, 2009 θ θ θ θ θ θ jn j n jn n n j j j e e T T e e T T e T T e T T − − ∞ = − − − − Γ Γ − Γ + Γ = Γ Γ Γ + Γ = ⋅⋅ ⋅ + Γ Γ + Γ + Γ = Γ 3 2 2 1 12 12 1 0 3 2 2 3 21 12 1 4 2 2 3 21 12 2 1 12 12 1 1 Podstawiaj c T12 przez 1 + Γ2 = 1 - Γ1 i T21 przez 1 + Γ1 otrzymujemy: 5 θ θ j j e e 2 3 1 2 3 1 1 − − Γ Γ + Γ + Γ = Γ Je li |Γ1| i |Γ3| s du o mniejsze od jedno ci, doskonałym przybli eniem jest wyra enie θ j e 2 3 1 − Γ + Γ = Γ Je li |Γ1| = |Γ3| = 0.2, bł d wyznaczenia Γ nie przekracza 4%. b. Teoria aproksymacyjna transformatorów wielosekcyjnych N N L N L N n n n n n n Z Z Z Z Z Z Z Z Z Z Z Z ρ ρ ρ = + − = Γ = + − = Γ = + − = Γ + + 1 1 0 0 1 0 1 0 θ θ θ ρ ρ ρ ρ jN N j j e e e 2 4 2 2 1 0 − − − + ⋅⋅ ⋅ + + + = Γ 6 Załó my, e transformator spełnia nast puj cy rodzaj symetrii:
(…)
… z przybli onych
zale no ci:
Z1 = ZL1/4 Z03/4
Z2 = ZL3/4 Z01/4
Przykład:
ZL = 200 Ω
Z0 = 50 Ω
Z1 = 70.71 Ω
Z2 = 141.42 Ω
TECHNIKA B.W.CZ, 2009
8
Moduł współczynnika odbicia i straty powrotu
9
Transformator o charakterystyce maksymalnie płaskiej N = 2. |S21|. Straty mocy wywołane
niedopasowaniem
10
d. Transformator o charakterystyce równomiernie falistej (Czebyszewa)
Tn (
cos θ
cos θ
) = cos n(cos −1
)
cos θ…
… (cos θ )
Z − Z0
1
ρm = L
Z L + Z 0 T N (sec θ m )
ZL − Z0
ρ m −1
T N (sec θ m ) =
ZL + Z0
1
−1 Z L − Z 0
sec θ m = cos( cos
ρ m −1 )
N
ZL + Z0
Przykład:
N = 2, ρm = 0.1, ZL = 200 Ω, Z0 = 50 Ω
Z1 = 71.2 Ω
Z2 = 118.7 Ω
θm = 1.007
fd = 1.923 GHz
fg = 4.077 GHz
B = 2.12
TECHNIKA B.W.CZ, 2009
12
TECHNIKA B.W.CZ, 2009
13
Moduł współczynnika odbicia i straty powrotu
14
Straty mocy wywołane niedopasowaniem
15…
... zobacz całą notatkę






Komentarze użytkowników (0)