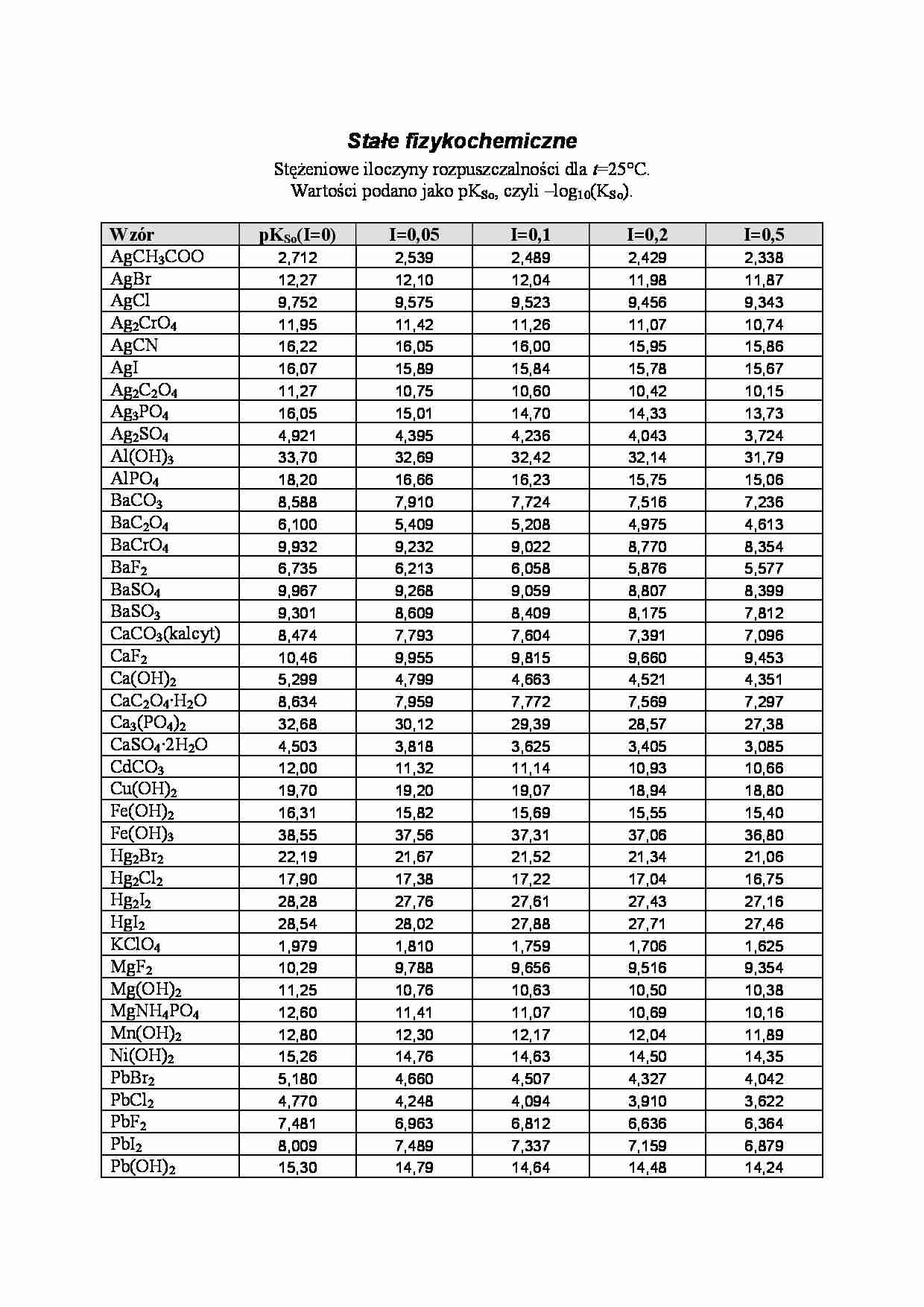
Stałe fizykochemiczne StęŜeniowe iloczyny rozpuszczalności dla t=25°C. Wartości podano jako pKSo, czyli –log10(KSo). Wzór pKSo(I=0) I=0,05 I=0,1 I=0,2 I=0,5 AgCH3COO 2,712 2,539 2,489 2,429 2,338 AgBr 12,27 12,10 12,04 11,98 11,87 AgCl 9,752 9,575 9,523 9,456 9,343 Ag2CrO4 11,95 11,42 11,26 11,07 10,74 AgCN 16,22 16,05 16,00 15,95 15,86 AgI 16,07 15,89 15,84 15,78 15,67 Ag2C2O4 11,27 10,75 10,60 10,42 10,15 Ag3PO4 16,05 15,01 14,70 14,33 13,73 Ag2SO4 4,921 4,395 4,236 4,043 3,724 Al(OH)3 33,70 32,69 32,42 32,14 31,79 AlPO4 18,20 16,66 16,23 15,75 15,06 BaCO3 8,588 7,910 7,724 7,516 7,236 BaC2O4 6,100 5,409 5,208 4,975 4,613 BaCrO4 9,932 9,232 9,022 8,770 8,354 BaF2 6,735 6,213 6,058 5,876 5,577 BaSO4 9,967 9,268 9,059 8,807 8,399 BaSO3 9,301 8,609 8,409 8,175 7,812 CaCO3(kalcyt) 8,474 7,793 7,604 7,391 7,096 CaF2 10,46 9,955 9,815 9,660 9,453 Ca(OH)2 5,299 4,799 4,663 4,521 4,351 CaC2O4·H2O 8,634 7,959 7,772 7,569 7,297 Ca3(PO4)2 32,68 30,12 29,39 28,57 27,38 CaSO4·2H2O 4,503 3,818 3,625 3,405 3,085 CdCO3 12,00 11,32 11,14 10,93 10,66 Cu(OH)2 19,70 19,20 19,07 18,94 18,80 Fe(OH)2 16,31 15,82 15,69 15,55 15,40 Fe(OH)3 38,55 37,56 37,31 37,06 36,80 Hg2Br2 22,19 21,67 21,52 21,34 21,06 Hg2Cl2 17,90 17,38 17,22 17,04 16,75 Hg2I2 28,28 27,76 27,61 27,43 27,16 HgI2 28,54 28,02 27,88 27,71 27,46 KClO4 1,979 1,810 1,759 1,706 1,625 MgF2 10,29 9,788 9,656 9,516 9,354 Mg(OH)2 11,25 10,76 10,63 10,50 10,38 MgNH4PO4 12,60 11,41 11,07 10,69 10,16 Mn(OH)2 12,80 12,30 12,17 12,04 11,89 Ni(OH)2 15,26 14,76 14,63 14,50 14,35 PbBr2 5,180 4,660 4,507 4,327 4,042 PbCl2 4,770 4,248 4,094 3,910 3,622 PbF2 7,481 6,963 6,812 6,636 6,364 PbI2 8,009 7,489 7,337 7,159 6,879 Pb(OH)2 15,30 14,79 14,64 14,48 14,24 PbSO4 7,597 6,903 6,699 6,455 6,069 SrCO3 9,252 8,564 8,368 8,140 7,807 SrC2O4 7,301 6,618 6,425 6,206 5,896 SrSO4 6,463 5,772
(…)
…–30 9,29·10–30
ZnS (sfaleryt) 2·10–4 2,95·10–4 3,29·10–4 3,71·10–4 4,37·10–4
2
fH
Korekcje dla zadanej siły jonowej obliczono w oparciu o wzór K = K (0) ⋅ , dla siarczków
fM
typu MS i jego analog dla Ag2S. Współczynniki aktywności obliczono w oparciu o metodę
SIT zakładając KNO3 jako elektrolit podstawowy.
Literatura:
R.J. Myers, J. Chem. Educ. 63 (1986) 687
The new low value for the second…
…)(I2-I1)(pK2–pK1)
a następnie K(I) = 10-pK(I)
Źródła danych :
D. Garwin, V.B. Parker, H.J. White, CODATA Thermodynamic Tables, Hemisphere, New
York, 1987 oraz 2000 CRC Press LLC i dane z bazy NIST (National Institute of Standards
and Technology).
Korekcje dla róŜnych sił jonowych obliczono programem Aq_Solutions zalecanym przez
Analytical Division of IUPAC (by I.V. Sukhno, V.Y. Buzko, L.D. Petit…
…
5,896
4,979
8,529
15,64
W celu interpolacji stałych naleŜy zastosować wzory:
pK(I) = pK(I1) + (I-I1)(I2-I1)(pK2–pK1)
a następnie K(I) = 10-pK(I)
Źródła danych :
D. Garwin, V.B. Parker, H.J. White, CODATA Thermodynamic Tables, Hemisphere, New
York, 1987 oraz 2000 CRC Press LLC i dane z bazy NIST (National Institute of Standards
and Technology).
Korekcje dla róŜnych sił jonowych obliczono programem…
…) przy uŜyciu metody
SIT: Specific Interaction Theory, zakładając jako elektrolit podstawowy KNO3.
Rozpuszczalność siarczków
Dla obliczania rozpuszczalności siarczków lepsze wyniki uzyskuje się w oparciu o stałe
równowagi roztwarzania:
MmSn(s) + 2n H+ (aq) <=> mM(2n/m)+ + n H2S(aq)
Wynika to z trudności eksperymentalnych i teoretycznych w wyznaczaniu drugiej stałej
dysocjacji kwasu siarkowodorowego.
Wzór osadu…
... zobacz całą notatkę





Komentarze użytkowników (0)