To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
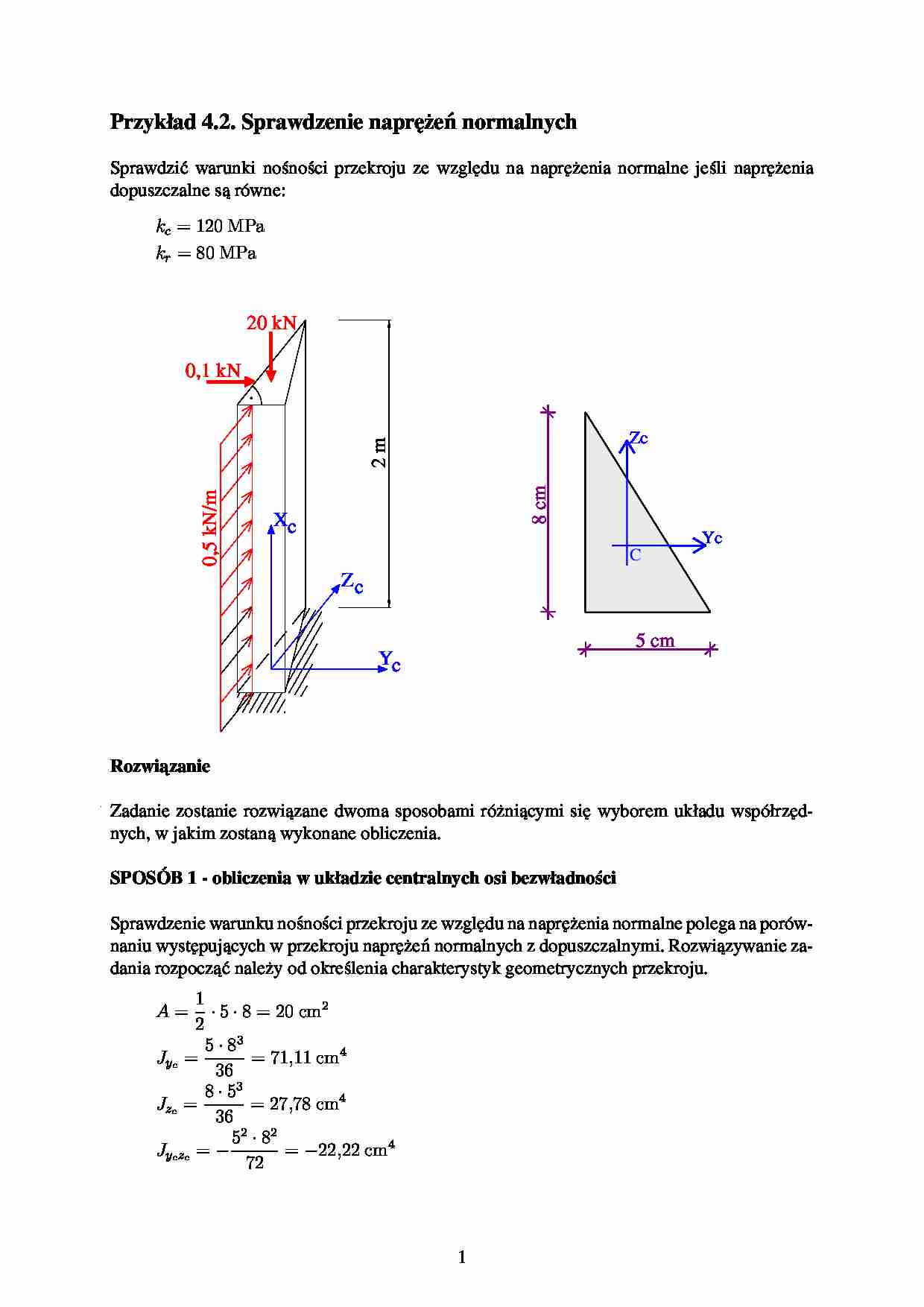


Przykład 4.2. Sprawdzenie napr˛ zen normalnych
e˙ ´
Sprawdzi´ warunki no´no´ci przekroju ze wzgl˛ du na napr˛ zenia normalne je´li napr˛ zenia
c
s s
e
e˙
s
e˙
dopuszczalne sa równe:
˛
kc = 120 MPa
kr = 80 MPa
20 kN
0,1 kN
8 cm
0,5 kN/m
2m
Zc
Xc
Yc
C
Zc
5 cm
Yc
Rozwiazanie
˛
Zadanie zostanie rozwiazane dwoma sposobami ró˙ niacymi si˛ wyborem układu współrz˛ d˛
z ˛
e
e
nych, w jakim zostana wykonane obliczenia.
˛
SPOSÓB 1 - obliczenia w układzie centralnych osi bezwładno´ci
s
Sprawdzenie warunku no´no´ci przekroju ze wzgl˛ du na napr˛ zenia normalne polega na poróws s
e
e˙
naniu wyst˛ pujacych w przekroju napr˛ zen normalnych z dopuszczalnymi. Rozwiazywanie zae ˛
e˙ ´
˛
dania rozpocza´ nale˙ y od okre´lenia charakterystyk geometrycznych przekroju.
˛c
z
s
1
· 5 · 8 = 20 cm2
2
5 · 83
Jy c =
= 71,11 cm4
36
8 · 53
Jz c =
= 27,78 cm4
36
52 · 82
= −22,22 cm4
Jy c z c = −
72
A=
1
W przekroju odległym o x ∈ 0; 2 m od podstawy słupa siły wewn˛ trzne maja warto´ c:
e
˛
s´
N = −20 kN
kN
1
kN
Myc = −0,5
· (2 m − x) · · (2 m − x) = −0,25
· (2 m − x)2
m
2
m
Mzc = 0,1 kN · (2 m − x)
Wyra´ nie wida´ , ze maksymalne warto´ci sił wewn˛ trznych wyst˛ puja dla x = 0, tj. w podz
c ˙
s
e
e ˛
stawie słupa, gdzie
N = −20 kN
kN
· (2 m − 0)2 = −1 kNm = −100 kNcm
m
Mzc = 0,1 kN · (2 m − 0) = 0,2 kNm = 20 kNcm
Myc = −0,25
M
8 cm
Zc
20 kNm
Yc
100 kNm
20 kN
5 cm
Wzór na napr˛ zenia normalne obowiazujacy dla centralnych osi bezwładno´ci ma posta´ :
e˙
˛ ˛
s
c
σx =
Jy z M z + J z c M y c
Jy z M y + J y c M z c
N
y− c c2 c
z
+ cc2 c
A
Jy c z c − J y c Jz c
Jy c z c − J y c Jz c
Podstawiajac obliczone warto´ci momentów bezwładno´ci i sił wewn˛ trznych otrzymujemy:
˛
s
s
e
−20 −22,22 · (−100) + 71,11 · 20
−22,22 · 20 + 27,78 · (−100)
yc −
zc =
+
2
20
(−22,22) − 71,11 · 27,78
(−22,22)2 − 71,11 · 27,78
= −1 − 2,46yc − 2,175zc
σx =
Równanie osi oboj˛ tnej otrzymujemy przyrównujac napr˛ zenie normalne σ x do zera.
e
˛
e˙
σx = 0
=⇒
=⇒
−1 − 2,46yc − 2,175zc = 0
yc
zc
+ 1 = 1 =⇒
1
−2,46
−2,175
=⇒
yc
zc
+
=1
−0,4065 −0,4598
Tak wi˛ c o´ oboj˛ tna przechodzi przez punkty (0; −0,4598 cm) i (−0,4065 cm; 0).
e s
e
2
ZB
M
8 cm
Zc
Y
Yc
C
oC
so
A
bo
5 cm
jet
na
Na powy˙ szym rysunku pokazano oprócz poło˙ enia osi oboj˛ tnej równie˙ wypadkowy wektor
z
z
e
z
momentu zginajacego oraz główne centralne osie bezwładno´ci (ich poło˙ enie wyznaczane jest
˛
s
z
przy okazji oblicze´ wykonywanych sposobem 2). Zrobiono to w celu sprawdzenia poprawn
no´ci oblicze´ . W przypadku zginania uko´nego jest bowiem reguła, ze o´ oboj˛ tna przekroju
s
n
s
˛ ˙ s
e
odchyla si˛ od kierunku wypadkowego momentu zginajacego w kierunku osi minimalnego moe
˛
mentu bezwładno´ci. W rozpatrywanym przypadku zasada ta jest spełniona (moment J z
... zobacz całą notatkę






Komentarze użytkowników (0)