To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
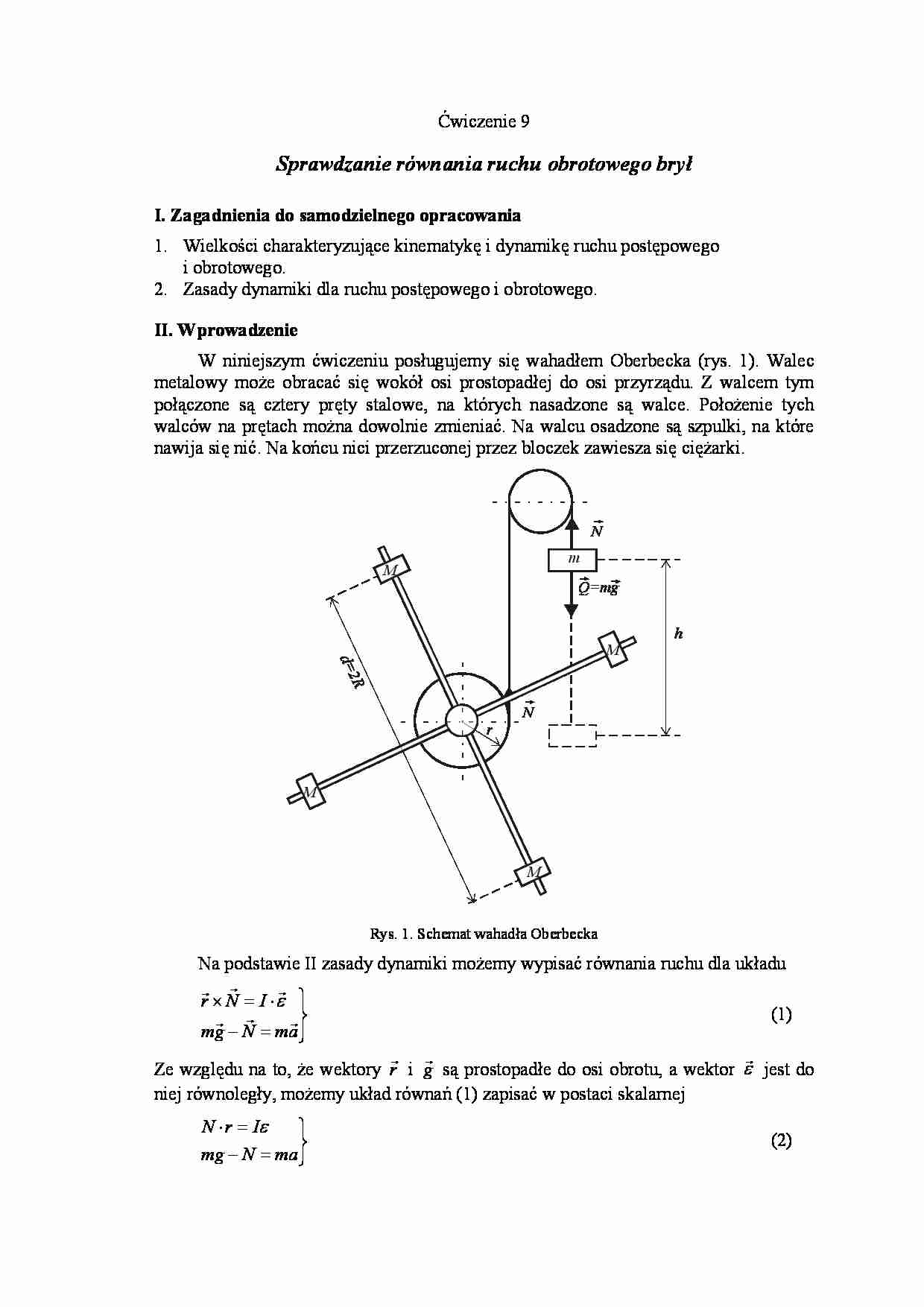


Ćwiczenie 9 Sprawdzanie równania ruchu obrotowego brył I. Zagadnienia do samodzielnego opracowania 1. Wielkości charakteryzujące kinematykę i dynamikę ruchu postępowego i obrotowego. 2. Zasady dynamiki dla ruchu postępowego i obrotowego. II. Wprowadzenie W niniejszym ćwiczeniu posługujemy się wahadłem Oberbecka (rys. 1). Walec metalowy może obracać się wokół osi prostopadłej do osi przyrządu. Z walcem tym połączone są cztery pręty stalowe, na których nasadzone są walce. Położenie tych walców na prętach można dowolnie zmieniać. Na walcu osadzone są szpulki, na które nawija się nić. Na końcu nici przerzuconej przez bloczek zawiesza się ciężarki. M M M M d=2 R m h r N Q=mg N Rys. 1. Schemat wahadła Oberbecka Na podstawie II zasady dynamiki możemy wypisać równania ruchu dla układu = − ⋅ = × a m N g m I N r r r r r r r ε (1) Ze względu na to, że wektory r r i g r są prostopadłe do osi obrotu, a wektor εr jest do niej równoległy, możemy układ równań (1) zapisać w postaci skalarnej = − = ⋅ ma N mg I r N ε (2) 2 Uwzględniając, że: r a = ε oraz 2 2 t h a = gdzie: h – wysokość spadania, t – czas spadania rozwiązując układ równań (2) obliczamy 2 t J mgr h g h t ⋅ + = 2 2 2 2 (3) Moment bezwładności układu I równy jest sumie momentów stałej części 0 I i walców w I . w 0 I I I + = Moment bezwładności walców w I zgodnie z prawem Steinera wynosi: 2 1 4 4 R M I Iw + = gdzie: 1 I - moment bezwładności walca W względem osi przechodzącej przez środek ciężkości i równoległej do osi obrotu przyrządu, M - masa walca W, R - odległość środka ciężkości walca od osi obrotu. Ze względów praktycznych odległość R zastępujemy odległością przeciwległych walców d ( ) R d 2 = . Zatem całkowity moment bezwładności wyraża się wzorem: 2 1 0 4 d M I I I + + = (4a) Pierwsze dwa wyrazy po prawej stronie w wyrażeniu (4a) są wielkościami stałymi. Wprowadzamy, więc oznaczenie 1 0 4 I I Ic + = i otrzymujemy: 2 d M I I c + =
... zobacz całą notatkę






Komentarze użytkowników (0)