To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
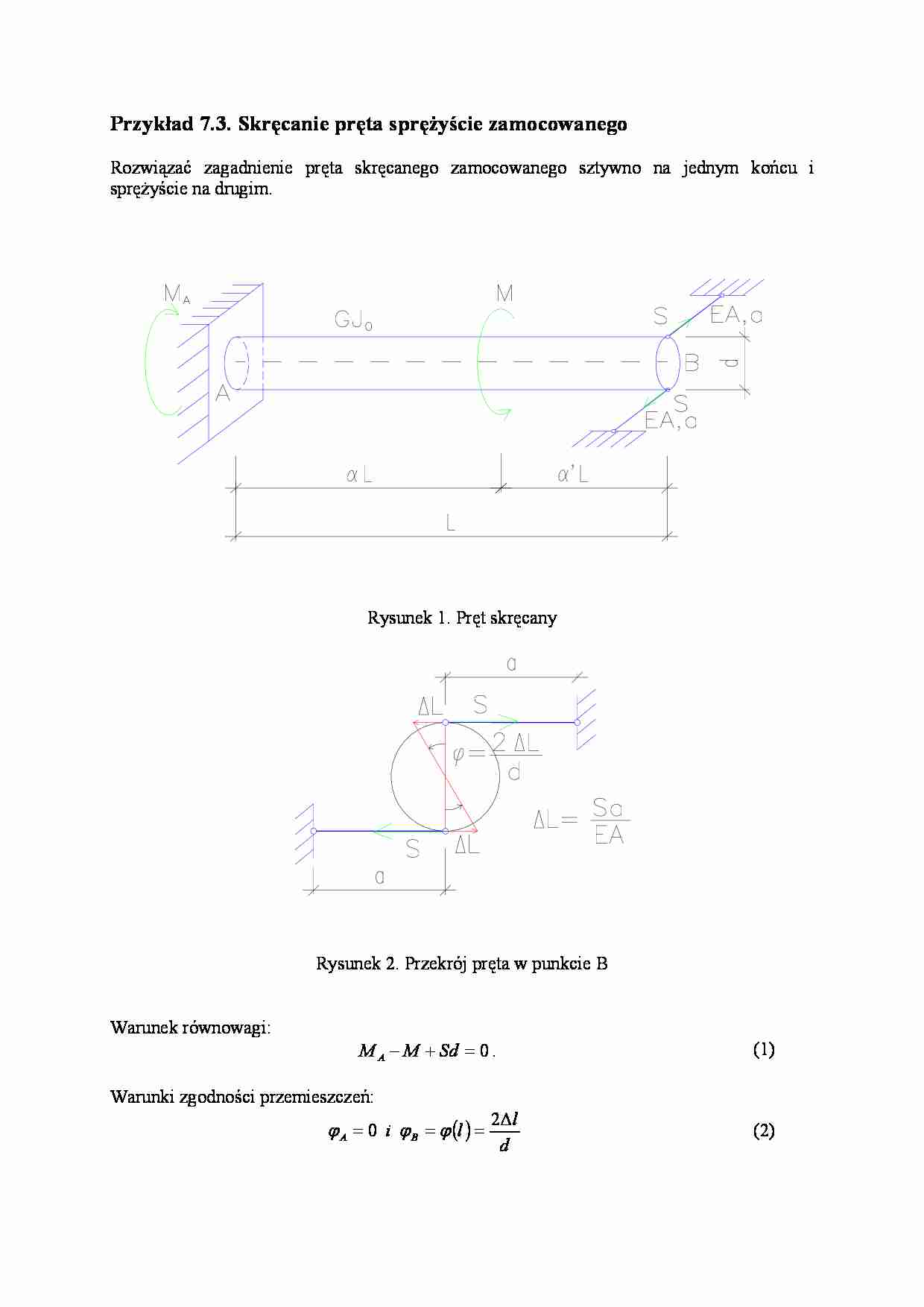


Przykład 7.3. Skręcanie pręta sprężyście zamocowanego
Rozwiązać zagadnienie pręta skręcanego zamocowanego sztywno na jednym końcu i
sprężyście na drugim.
Rysunek 1. Pręt skręcany
Rysunek 2. Przekrój pręta w punkcie B
Warunek równowagi:
M A − M + Sd = 0 .
Warunki zgodności przemieszczeń:
ϕ A = 0 i ϕ B = ϕ (l ) =
2 ∆l
d
(1)
(2)
Obliczymy:
Zatem,
M A l Mα ' l
2 Sa
, ϕB =
−
GJ 0
GJ 0
d EA
(3)
M Al Mα ' l 2 Sa
−
=
GJ 0
GJ 0
d EA
ϕB =
(4)
lub
M A − Mα ' =
2 SaGJ 0
i M A − M = − Sd .
d EAl
Odejmując stronami powyższe równania otrzymujemy:
a G J0
Mα = S d + 2
.
d E Al
(5)
(6)
Tak, więc:
1
αd
S = Mα
, M A = M 1 −
a J0 G
d + 2 a J0 G
d +2
d Al E
d Al E
(7)
Mamy dwa graniczne przypadki szczególne:
1. K s = GJ 0 / l K r = EA / a , tzn. mamy przypadek odwrotny. Wtedy rozwiązania dążą do
(9)
Mα K r 2
Sd →
d → 0 , MA = M
2 Ks
Rysunek 4. Wykres momentu skręcającego
2
W ogólnym przypadku mamy:
1
α
,
Sd = Mα
, M A = M 1 −
1 Ks
1 Ks
1+ 2 2
1+ 2 d 2 K
d Kr
r
(10)
gdzie
GJ 0
EA
(9)
, Kr =
l
a
są sztywnościami pręta skręcanego i rozciąganego, odpowiednio. Wykresy momentu
skręcającego i kąta skręcenia mają postać:
Ks =
Rysunek 5. Wykresy momentu skręcającego i kąta skręcenia
Tablica 1 Charakterystyki geometryczne przekroju w zagadnieniu skręcania:
Przekrój
Moment bezwładności
πr 4 πd 4
J0 =
=
2
32
3
Wskaźnik wytrzymałości
J 0 πr 3 πd 3
WS =
=
=
2
16
r
πR 4 πr 2 πR 4
(1 − m 4 )
J0 =
=
2 2
2
4
πD
(1 − m 4 ) ,
J0 =
32
r d
m = =
... zobacz całą notatkę






Komentarze użytkowników (0)