

Fragment notatki:
4.1. Doświadczenie Reynoldsa
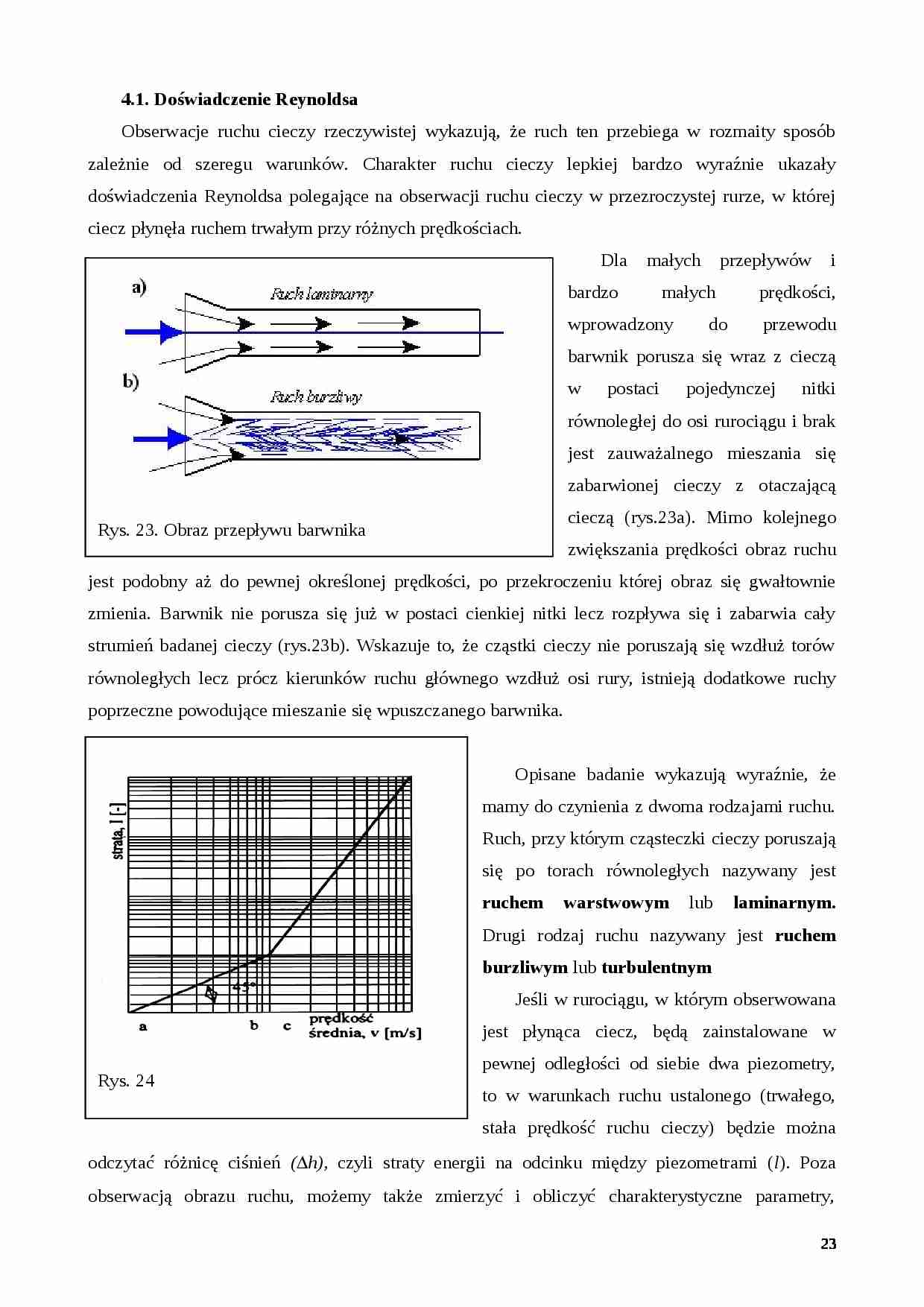
Obserwacje ruchu cieczy rzeczywistej wykazują, że ruch ten przebiega w rozmaity sposób zależnie od szeregu warunków. Charakter ruchu cieczy lepkiej bardzo wyraźnie ukazały doświadczenia Reynoldsa polegające na obserwacji ruchu cieczy w przezroczystej rurze, w której ciecz płynęła ruchem trwałym przy różnych prędkościach.
Dla małych przepływów i bardzo małych prędkości, wprowadzony do przewodu barwnik porusza się wraz z cieczą w postaci pojedynczej nitki równoległej do osi rurociągu i brak jest zauważalnego mieszania się zabarwionej cieczy z otaczającą cieczą (rys.23a). Mimo kolejnego zwiększania prędkości obraz ruchu jest podobny aż do pewnej określonej prędkości, po przekroczeniu której obraz się gwałtownie zmienia. Barwnik nie porusza się już w postaci cienkiej nitki lecz rozpływa się i zabarwia cały strumień badanej cieczy (rys.23b). Wskazuje to, że cząstki cieczy nie poruszają się wzdłuż torów równoległych lecz prócz kierunków ruchu głównego wzdłuż osi rury, istnieją dodatkowe ruchy poprzeczne powodujące mieszanie się wpuszczanego barwnika.
Opisane badanie wykazują wyraźnie, że mamy do czynienia z dwoma rodzajami ruchu. Ruch, przy którym cząsteczki cieczy poruszają się po torach równoległych nazywany jest ruchem warstwowym lub laminarnym. Drugi rodzaj ruchu nazywany jest ruchem burzliwym lub turbulentnym
Jeśli w rurociągu, w którym obserwowana jest płynąca ciecz, będą zainstalowane w pewnej odległości od siebie dwa piezometry, to w warunkach ruchu ustalonego (trwałego, stała prędkość ruchu cieczy) będzie można odczytać różnicę ciśnień (Δh), czyli straty energii na odcinku między piezometrami (l). Poza obserwacją obrazu ruchu, możemy także zmierzyć i obliczyć charakterystyczne parametry, opisujące warunki przeprowadzanego doświadczenia. Będą to następujące wielkości: prędkość średnia przepływu cieczy v, otrzymana z bezpośredniego pomiaru objętości cieczy V wypływającej z rurociągu o znanej średnicy w określonym czasie Δt, i jednostkowe straty energii Δh/l. Wyniki pomiarów można nanieść na wykres. Otrzymaną krzywą można opisać równaniem lub po logarytmowaniu obu stron równania w postaci lg I = lg a + n lg v.
Wykres uzyskanej krzywej w układzie współrzędnych logarytmicznych przedstawiono na rys.24. W granicach prędkości od a do b prosta przebiega pod kątem 45°, tzn. wykładnik potęgowy n w zależności opisującej tę krzywą wynosi 1, natomiast przy prędkościach powyżej granicy c wykładnik ten przybiera wartość 2. W przedziale b - c, w tzw. obszarze przejściowym, punkty doświadczalne są dość rozproszone i ich położenie zależy czy w trakcie przeprowadzania doświadczenia kolejno zwiększaliśmy, czy zmniejszaliśmy prędkość. Prędkości określające ten obszar nazywane są
(…)
… Reynoldsa odpowiadające temu obszarowi określone są jako (Re)'gran < Re < (Re)''gran. W przypadku gdy zachodzi zależność 4000 ≤ Re ≤ (Re)'gran należy stosować w praktyce zależności dla rurociągów gładkich, natomiast dla Re ≥ (Re)''gran znajdujemy się w obszarze kwadratowej zależności oporów ruchu, czyli ruchu w pełni burzliwego. Wg Czugajewa można przyjmować następujące graniczne wartości liczb Reynoldsa…
….
4.2. Opory ruchu w ruchu laminarnym jednostajnym
Zakładamy, że rozpatrujemy przepływ w prostoosiowym poziomym przewodzie kołowym o promieniu ro, w którym wyodrębniamy powierzchnię walcową o promieniu r i długości l, współśrodkową z osią przewodu w którym charakterystyka prędkości ruchu cieczy nie zmienia się na długości przewodu. Jedynymi siłami działającymi na wydzielony walec cieczy, siłami…
… ruchu laminarnego tj. w granicach Re ≤ 2300.
5.3. Opory ruchu rurociągów hydraulicznie gładkich
W obszarze przejściowym, w granicach między ruchem laminarnym a ruchem w pełni burzliwym dla rurociągów hydraulicznie gładkich może być stosowany empiryczny wzór Blasiusa w postaci
(55)
Zależność ta może być stosowana w przedziale 4000 < Re < 100 000.
5.4. Opory liniowe w obszarze ruchu burzliwego
Pośród…
…/l. Równanie (37) nazywana jest podstawowym równaniem ruchu jednostajnego, ważnym dla przewodów pod ciśnieniem i dla koryt otwartych.
W wielu przypadkach korzystne jest stosowanie pojęcia prędkości dynamicznej vxdefiniowanej jako , co pozwala zapisać (38)
Powyżej przedstawione zależności ważne są dla ruchu laminarnego i burzliwego. W praktycznym zastosowaniu najczęściej spotykana jest zależność w której występuje współczynnik oporu liniowego λ, zwana wzorem Darcy-Weisbacha
(39)
Warto zauważyć, że jest ono równoważne zależności .
4.3. Rozkład prędkości w ruchu laminarnym
Dla ruchu jednostajnego ustalonego, wychodząc z newtonowskiej definicji lepkości cieczy (str. 2) oraz równania (37b), można na drodze teoretycznej wyprowadzić równanie określające rozkład prędkości w przekroju poprzecznym. Dla rurociągów…
… laminarny występuje gdy nie jest przekroczona liczba graniczna Re = 2320.
Praktycznie biorąc przepływy laminarne mogą występować najczęściej przy ruchu cieczy w kapilarach, w przepływach wód gruntowych, przepływach w warstwie przyściennej. W pełnym przekroju rurociągu ruch laminarny występuje raczej rzadko a wyjątkowo w przepływach cieczy w korytach otwartych (rowach, kanałach).
Parametrem, który pozwala…
… o promieniu ro = 0,5 d. Po przekształceniach otrzymujemy
(37a)
gdzie ro - naprężenia styczne przy ściankach rurociągu, A - pole przekroju poprzecznego, χ -obwód zwilżony a hf - straty wysokości ciśnienia na opory tarcia na długości rurociągu l. Równanie (37a), przedstawiane jest w postaci
(37b)
gdzie promień hydrauliczny Rh = A/χ a spadek hydrauliczny (jednostkowe straty energii na długości rurociągu) I = h…
... zobacz całą notatkę

Komentarze użytkowników (0)