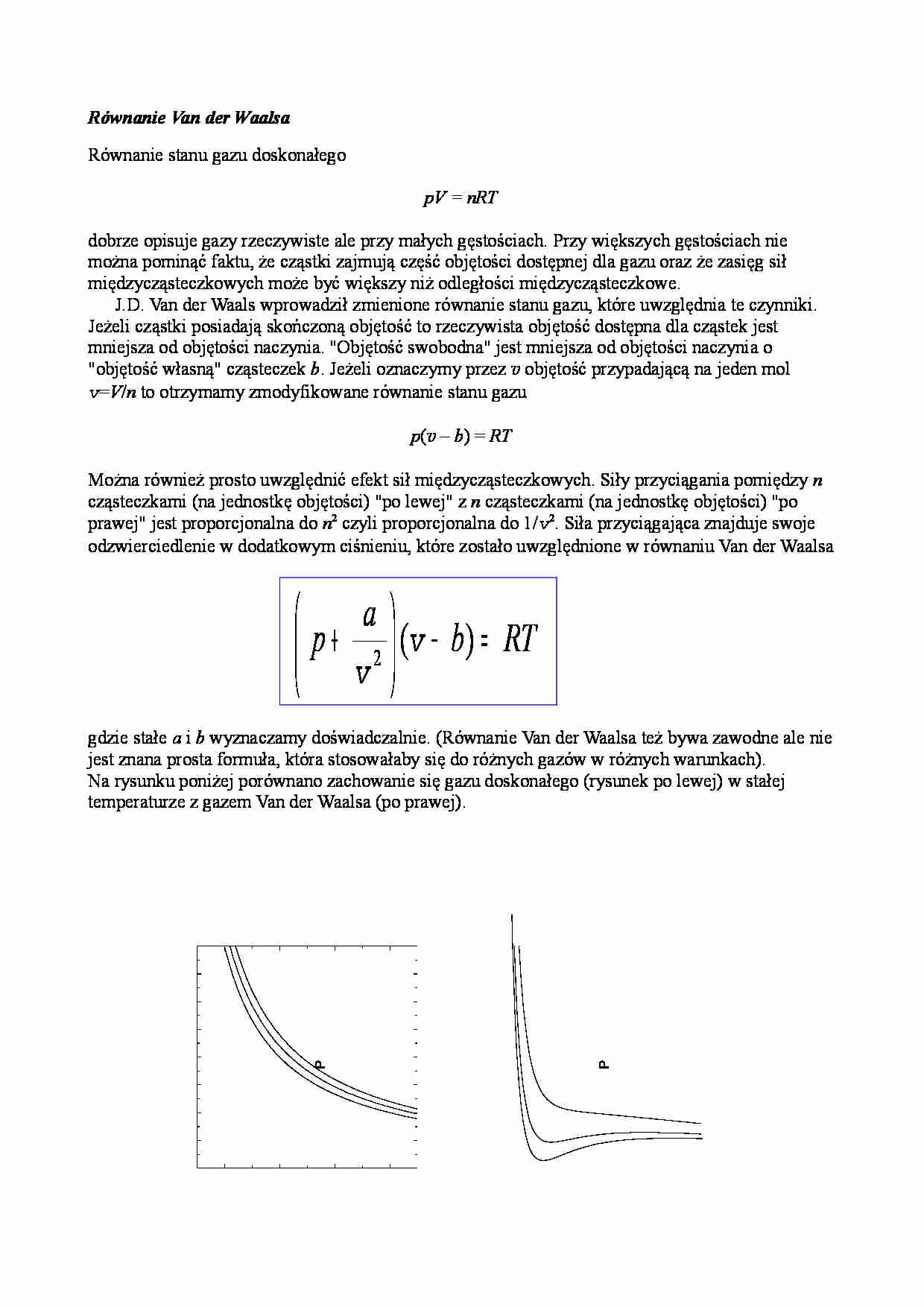
Równanie Van der Waalsa

Równanie Van der Waalsa Równanie stanu gazu doskonałego pV = nRT dobrze opisuje gazy rzeczywiste ale przy małych gęstościach. Przy większych gęstościach nie  można pominąć faktu, że cząstki zajmują część objętości dostępnej dla gazu oraz że zasięg sił  międzycząsteczkowych może być większy niż odległości międzycząsteczkowe. J.D. Van der Waals wprowadził zmienione równanie stanu gazu, które uwzględnia te czynniki.  Jeżeli cząstki posiadają skończoną objętość to rzeczywista objętość dostępna dla cząstek jest  mniejsza od objętości naczynia. "Objętość swobodna" jest mniejsza od objętości naczynia o  "objętość własną" cząsteczek  b . Jeżeli oznaczymy przez  v  objętość przypadającą na jeden mol  v = V / n  to otrzymamy zmodyfikowane równanie stanu gazu p ( v – b ) =  RT Można również prosto uwzględnić efekt sił międzycząsteczkowych. Siły przyciągania pomiędzy  n  cząsteczkami (na jednostkę objętości) "po lewej" z  n  cząsteczkami (na jednostkę objętości) "po  prawej" jest proporcjonalna do  n 2 czyli proporcjonalna do 1/ v 2. Siła przyciągająca znajduje swoje  odzwierciedlenie w dodatkowym ciśnieniu, które zostało uwzględnione w równaniu Van der Waalsa RT b a p = −       + ) ( 2 v v gdzie stałe  a  i  b  wyznaczamy doświadczalnie. (Równanie Van der Waalsa też bywa zawodne ale nie  jest znana prosta formuła, która stosowałaby się do różnych gazów w różnych warunkach). Na rysunku poniżej porównano zachowanie się gazu doskonałego (rysunek po lewej) w stałej  temperaturze z gazem Van der Waalsa (po prawej). 0.05 0.10 0.15 0.20 0 50 100 150 200 250 300 350 400 P V 0.05 0.10 0.15 0.20 0 50 100 150 200 250 300 350 400 P V Document Outline Równanie Van der Waalsa ... zobacz całą notatkę