To tylko jedna z 14 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Poj cia i zagadnienia do wykładu:
-) teoria kinetyczno-cz steczkowa gazów;
-) liczba Loschmidta;
-) stała Boltzmanna (k);
-) rednia droga swobodna;
-) rednia liczba zderze cz steczek;
-) g sto
gazów;
-) gazy rzeczywiste;
-) temperatura Boyle’a;
W
teorii
kinetyczno-cz steczkowej
gazów,
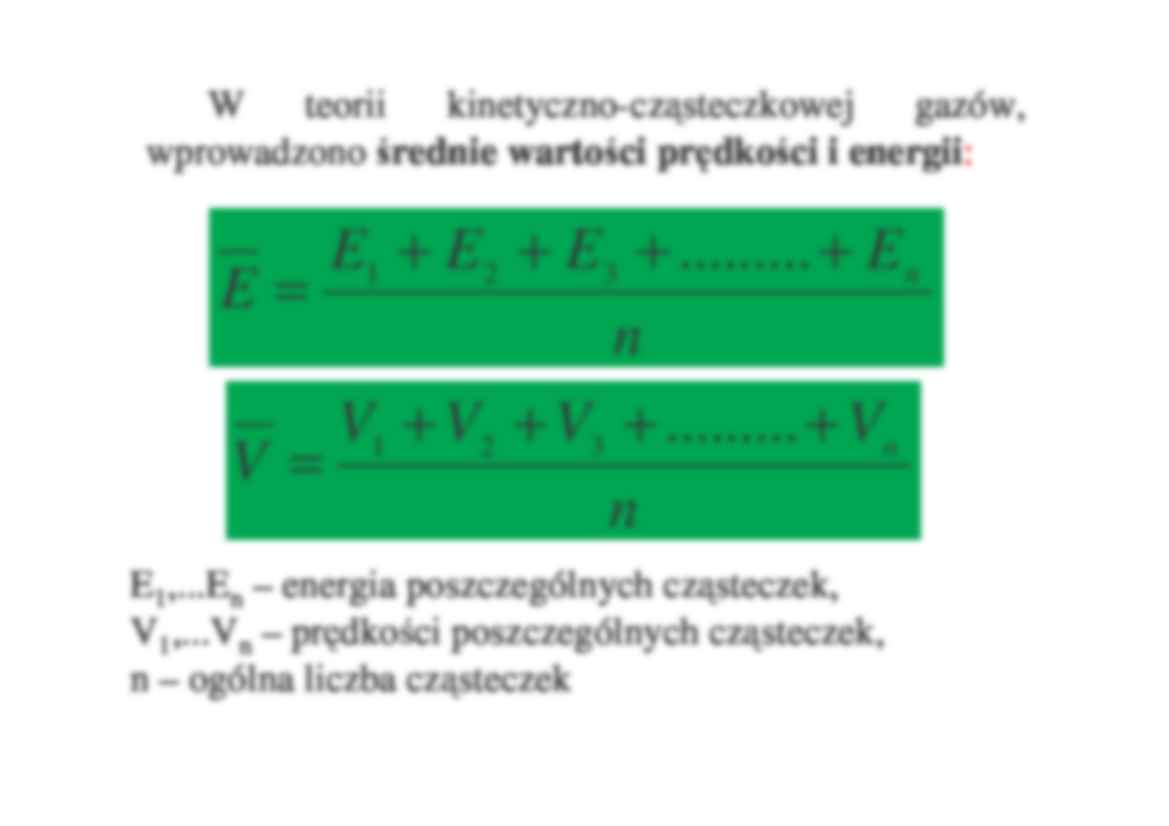
wprowadzono rednie warto ci pr dko ci i energii:
E1 + E 2 + E3 + ......... + E n
E=
n
V1 + V2 + V3 + ......... + Vn
V=
n
E1,...En – energia poszczególnych cz steczek,
V1,...Vn – pr dko ci poszczególnych cz steczek,
n – ogólna liczba cz steczek
Z oblicze wynika, e rednia energia kinetyczna 1
mola wyra a si wzorem:
3
E = RT
2
3 RT
E=
2 N
Iloraz R/N jest to stała Boltzmanna (k):
k = 1,38054·10-23 J/K
wtedy rednia energia kinetyczna wynosi:
3
E i = kT
2
ułamek liczby cz steczek, Ni/N
Rozkład pr dko ci cz steczek tlenu w 00C i -2000C
pr dko , V [m/s]
G sto
g sto
bezwzgl dna
d = m/v
i masa molowa gazów
g sto
wzgl dna
dwzg = dx/dpowietrza
dwzg’ = dx/dH2
Gazy rzeczywiste. Równanie van der Waalsa
Im ni sza jest temperatura i wy sze ci nienie gazu,
tym gaz wykazuje wi ksze odst pstwa od praw gazu
doskonałego.
iloczyn, pv
Zale no iloczynu ci nienia i obj to ci od ci nienia dla
gazów rzeczywistych
ci nienie, p
Van der Waals zaproponował, aby w przypadku
gazów rzeczywistych zamiast ci nienia stosowa :
a
p+ 2
V
Druga poprawka, uwzgl dniała sko czon obj to
cz steczek gazu rzeczywistego: V-b
b – stała, zale na od wielko ci i kształtu cz steczek
a
( p + 2 ) ⋅ (V − b) = RT
V
Dla n moli gazu rzeczywistego:
an
( p + 2 ) ⋅ (v − nb) = nRT
v
2
Warto ci współczynników a i b w równaniu van der
Waalsa dla niektórych gazów
Gaz
a
[m6Pa/mol2]
b
[l/mol]
amoniak
azot
dwutlenek w gla
hel
tlen
woda
wodór
0,422
0,141
0,036
0,0034
0,1378
0,579
0,0248
0,05136
0,03913
0,04267
0,02370
0,03183
0,0319
0,02661
Równanie van der Waalsa:
Równanie Berthelota:
Równanie
Dietericiego:
RT
a
p=
− 2
V −b V
RT
a
p=
−
2
V − b TV
− a / RTV
RTe
p=
V −b
Równanie
BeattieBridgmana:
(1 − γ ) RT (v + β ) − α
p=
2
V
dla
a
α = a 0 (1 + ),
V
b
β = b0 (1 − ),
V
c0
γ =
3
VT
Równanie wirialne (Kammerlingh Onnes):
RT
B(T ) C (T )
p=
{1 +
+ 2 + ........}
V
V
V
... zobacz całą notatkę






Komentarze użytkowników (0)