To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
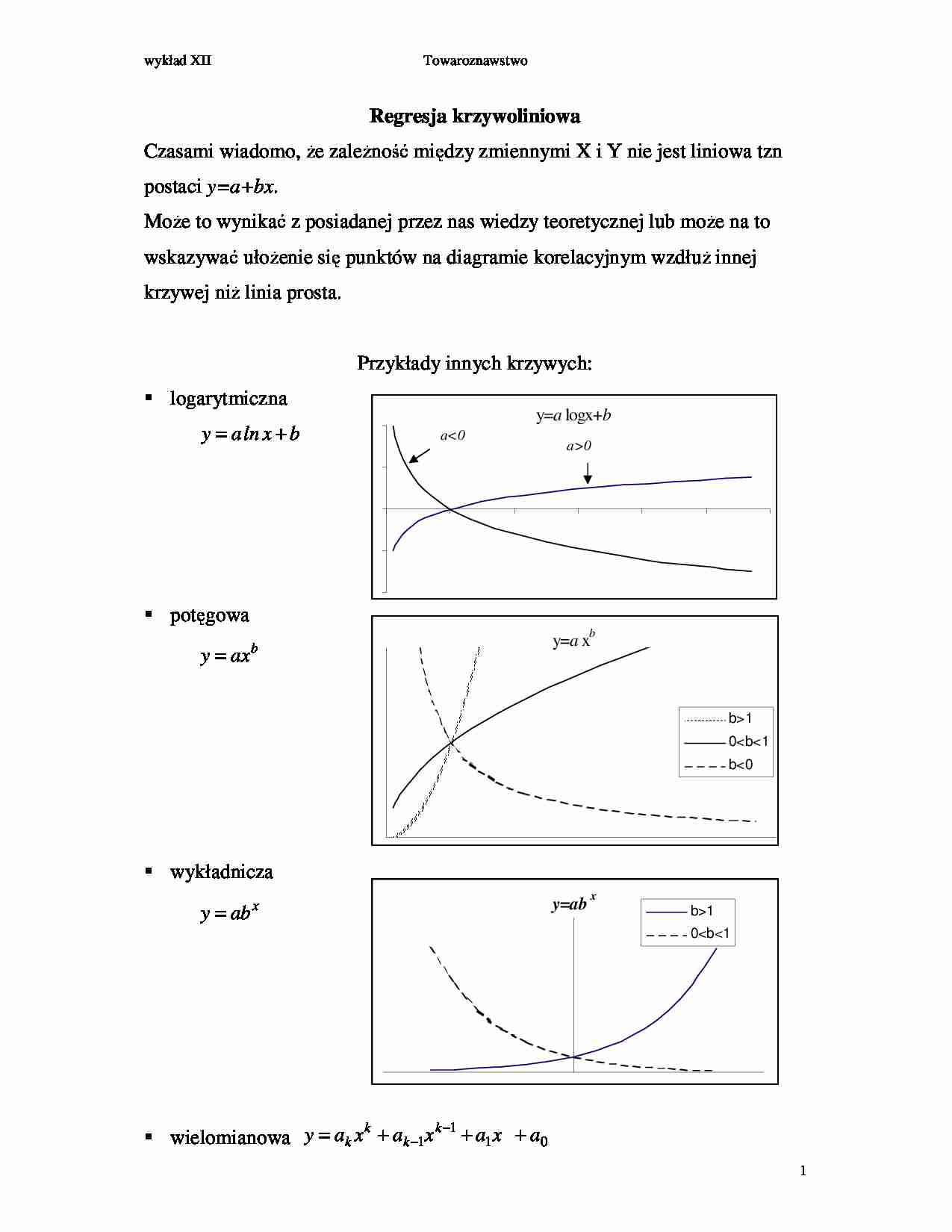


wykład XII Towaroznawstwo 1 Regresja krzywoliniowa Czasami wiadomo, e zale ność między zmiennymi X i Y nie jest liniowa tzn postaci y=a+bx . Mo e to wynikać z posiadanej przez nas wiedzy teoretycznej lub mo e na to wskazywać uło enie się punktów na diagramie korelacyjnym wzdłu innej krzywej ni linia prosta. Przykłady innych krzywych: logarytmiczna b x ln a y + = potęgowa b ax y = wykładnicza x ab y = wielomianowa 0 1 1 1 a x a x a x a y k k k k + + + = − − y= a logx+ b a0 y= a x b b1 01 0
(…)
…
Te reszty powinny być losowe tzn równomiernie rozło one wokół zera. Są
specjalne testy (testy serii) badające losowość reszt.
Jak dopasować krzywą metodą najmniejszych kwadratów?
W naszym przykładzie szukamy takich wartości a i b , e wartość
n
∑ (y
ˆ
− yi ) gdzie yi = a + b ln x
ˆ
2
i
i =1
osiąga minimum
Na ogół u ywa się do rozwiązania tego zagadnienia programów komputerowych
(np Excela).
3
wykład XII…
… 2,34
składnika (Y)
Współczynnik korelacji Pearsona dla powy szych danych wynosi 0,939.
Wydawać by się mogło, e jest silna zale ność liniowa między X i Y. Diagram
korelacyjny z dopasowaną linią
3 ,5
y = 0 ,4 2 2 1 x - 0 ,9 1 4
2
R = 0 ,8 8 2
3
Widać, e linia prosta zupełnie nie
pasuje do punktów na wykresie.
zmiana składnika krwi
prostą wygląda następująco:
2 ,5
2
1 ,5
1
0 ,5
0
- 0 ,5 0
2
4
6
8
10
-1…
… dopasowania danych do znalezionego równania jest współczynnik
determinacji:
n
∑ (ˆy
R2 =
i =1
n
i
− y )2
∑ ( y i − y )2
.
i =1
4
wykład XII
Towaroznawstwo
Przykład
Badając zanieczyszczenia terenu wokół pewnego obiektu przemysłowego
odsłonięto 7 profili glebowych. W powierzchniowej warstwie badanych profili
zawartości ołowiu, cynku i miedzi (w mg/kg) były następujące:
Pb (X1) 355 190 345 316 269 248 275
Zn…
… widzimy współczynniki równania oraz to , e tylko
współczynnik stojący przy Pb jest istotny statystycznie. Tak więc tylko
zale ność Cu od Pb powinna być brana pod uwagę. W tej sytuacji powtórzmy
całą analizę rezygnując ze zmiennej Zn. To będzie ju zwykła regresja liniowa
(nie wielokrotna). Otrzymujemy w Excelu:
6
wykład XII
Towaroznawstwo
ANALIZA WARIANCJI
df
Regresja
1
Resztkowy
5
Razem
6
SS
MS
F…
... zobacz całą notatkę






Komentarze użytkowników (0)