To tylko jedna z 11 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Przykład korekcji szeregowej członem proporcjonalnym
Jeżeli znany jest nam model obiektu możemy posłużyć się symulacją utworzoną w SIMULINKU. Użycie tego składnika programu MATLAB pozwala w krótkim czasie przeprowadzić wiele symulacji. Jest to narzędzie bardzo wygodne, posiadające ogromne możliwości. Jest również atrakcyjne pod względem wizualnym. Daje intuicyjny obraz złożonego układu regulacji. Posiada znaczny zasób źródeł sygnałów oraz innych bloków funkcjonalnych pozwalających budować ogromną ilość modeli. Aby przybliżyć działanie programu SIMULINK pakiet PDA został zaopatrzony w różne przykładowe symulacje. Aby uruchomić przykładową symulację wpisujemy symulacja z linii poleceń Matlaba (pliki simulink mają postać *.mdl). Edytując pola obiektu, zadajnika i czujnika wprowadzamy parametry modelu (najpierw należy uruchomić pda ). Niech
- transmitancja zadajnika ,
- transmitancja obiektu głównego,
- transmitancja czujnika ,
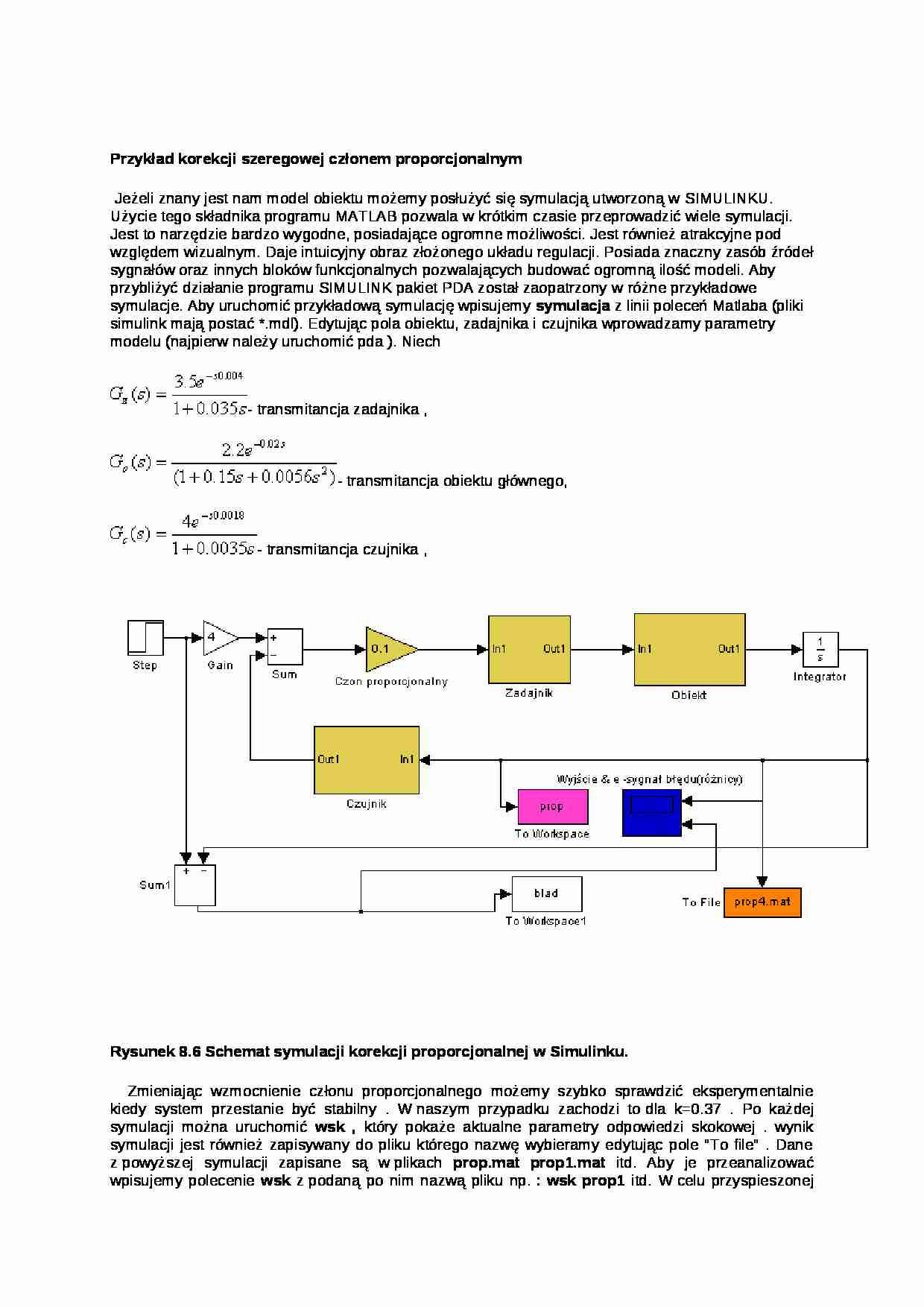
Rysunek 8.6 Schemat symulacji korekcji proporcjonalnej w Simulinku.
Zmieniając wzmocnienie członu proporcjonalnego możemy szybko sprawdzić eksperymentalnie kiedy system przestanie być stabilny . W naszym przypadku zachodzi to dla k=0.37 . Po każdej symulacji można uruchomić wsk , który pokaże aktualne parametry odpowiedzi skokowej . wynik symulacji jest również zapisywany do pliku którego nazwę wybieramy edytując pole "To file" . Dane z powyższej symulacji zapisane są w plikach prop.mat prop1.mat itd. Aby je przeanalizować wpisujemy polecenie wsk z podaną po nim nazwą pliku np. : wsk prop1 itd. W celu przyspieszonej analizy możemy posłużyć się skryptem regp1 . Musimy wprowadzić do Matlaba transmitancję naszych obiektów . Pomocniczy skrypt do tego celu to trans , edytując go wprowadzamy w odpowiednie miejsca transmitancje i opóźnienia odpowiednich członów . Rysunek 8.7 Wykresy przeregulowania oraz czasów regulacji w funkcji wzmocnienia
Wykonując to polecenie a następnie uruchamiając skrypt regp1 otrzymamy wykresy przeregulowania oraz czasów ustalania w funkcji wzmocnienia w torze głównym .
Widzimy tu optymalny czas regulacji T5% dla wzmocnienia k=0.07 . Możemy edytować skrypt trans wstawiając w odpowiednie miejsce k=0.07 i w przestrzeni roboczej Matlaba znajdzie się transmitancja układu zamkniętego H(s) . Aby poznać parametry odpowiedzi skokowej należy wykonać sgen ; wsk; . Czas regulacji wynosi T5=0.86 s. Wykonaliśmy w ten sposób pierwszy projekt regulatora proporcjonalnego .
W przypadku tego typu regulacji możemy wyciągnąć następujący wniosek; - zwiększanie wzmocnienia w torze głównym powoduje zwiększenie przeregulowania, w konsekwencji doprowadzi do destabilizacji obiektu.
(…)
… (skryptem) Matlabowym "regp.m'. Wykorzystuje on do wyznaczania parametrów odpowiedzi skokowej funkcję "wskjak.m" (wskaźniki jakości bez rysowania wykresu).
Rysunek 9.4 Wykresy przeregulowania oraz czasów regulacji w funkcji stałej Ti Wykresy przedstawiają zależność przeregulowania k oraz czasów regulacji TD w funkcji stałej całkowania Ti regulatora. Minimum T5% uzyskujemy dla Ti =240s. Podstawiając tę…
… członu do układu spowodowało, iż uchyb pozycyjny jest zerowy bez względu na wzmocnienie układu otwartego.
W ten oto sposób wykonaliśmy pierwszy projekt regulatora a w zasadzie korektora (używamy jednej nastawy stałej całkowania) poprawiającego dokładność (zapewnia zerowy uchyb pozycyjny).
Pominąłem omówienie programu Zerpol Dodatek A. Transmitancja drugiego rzędu
Rozpatrzmy obiekt o transmitancji…
… tak, aby wartość końcowa wynosiła 1. Dlatego wyznaczymy wartość ustaloną odpowiedzi skokowej. Układ zamknięty jest stabilny zatem możemy skorzystać z twierdzenia o wartości granicznej:
Zatem uchyb położeniowy (na pobudzenie skokiem jednostkowym) wynosi 1-0.58=0.42. Czas ustalania T5%=105s.
Rysunek 9.2 Odpowiedź skokowa układu zamkniętego bez regulatora
Zbadajmy teraz układ z regulatorem. Zauważmy, że układ otwarty jest niestabilny (biegun wnoszony przez niestabilny człon GR leży w początku układu współrzędnych na płaszczyźnie 's'). Transmitancja układu zamkniętego:
co po podstawieniu daje Układ zamknięty jest stabilny (polecenie pole(G(s) pokaże wartości biegunów). Możemy skorzystać z twierdzenia o wartości granicznej transformaty: ,
co oznacza, że pobudzenie skokiem o wysokości '1' (R(s)=1/s) otrzymamy…
… .
Jest to transmitancja drugiego rzędu ze stałym licznikiem. Posiada ona dwa bieguny i nie posiada zer. Jej bieguny to gdzie stałe:
współczynnik tłumienia, n pulsacja naturalna (pulsacja drgań nietłumionych), σ tłumienie, d pulsacja drgań tłumionych. Na rysunku 10.1 jest pokazane rozmieszczenie biegunów transmitancji na płaszczyźnie 's'. Rysunek 10.1 Położenie biegunów transmitancji drugiego rzędu na płaszczyźnie…
... zobacz całą notatkę






Komentarze użytkowników (0)