To tylko jedna z 14 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę

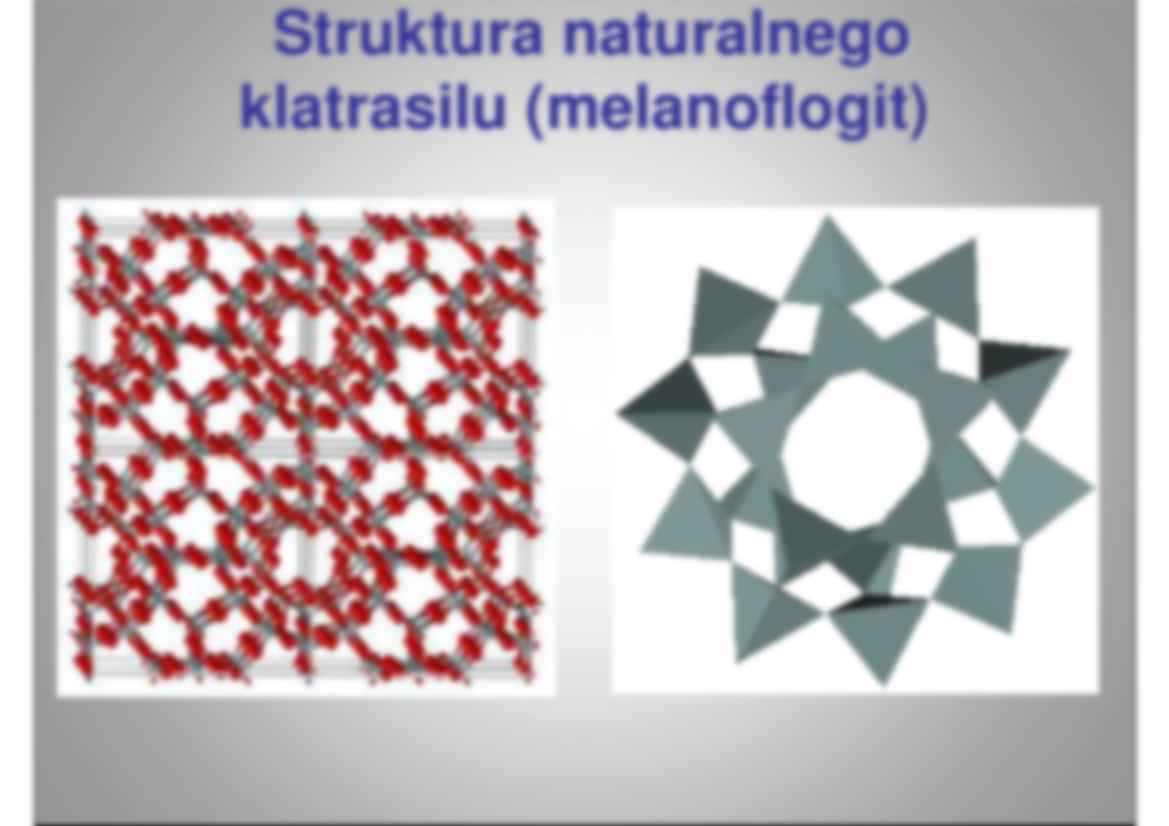

1. Przekształcenia izometryczne 2. Operacje symetrii mo Ŝ liwe w sieci 3. Iloczyn przekształce ń 4. Symbole elementów symetrii Wyk Wy ład 3 ad Przekszta Przekszt łcenia izometryczne w sieci cenia izometryczne w sieci krystalicznej krystaliczne Struktura naturalnego Struktura naturalnego klatrasilu (melanoflogit) klatrasilu (melanoflogit Przekszta Przekszt łcenia izometryczne cenia izometryczne Przekszta łcenie izometryczne ( z grec. izo- ten sam , metri – odległo ść ;) to przekształcenie, które w wyniku jego zastosowania nie powoduje zmian odległo ś ci mi ę dzy dwoma dowolnymi, przekształcanymi punktami: → → r = T(r) gdzie: → r - odległość między dowolnymi dwoma punktami, → T(r) - odległość między tymi samymi punktami po przekształceniu T Translacja i operacje symetrii Translacja i operacje symetri Zamkni ę te 1. o ś obrotu 2. centrum inwersji (symetrii) 3. płaszczyzna symetrii 4. o ś inwersyjna (obrót i odbicie w centrum) Otwarte 1. o ś ś rubowa ( obrót + translacja) 2. płaszczyzna po ś lizgowa (odbicie + translacja) Obr Ob ót wok t wo ół osi os Osie obrotu w sieci Osie obrotu w siec CD = k·AB gdzie: k - liczba całkowita, CD = CE + EF + FD natomiast: EF = AB z definicji funkcji cosinus oraz ujemnej wartości tej funkcji w przedziale kątowym 180-270o: CE = FD = -AB·cos ϕ z powyŜszych równań moŜna wyprowadzić zaleŜność: k·AB = AB + 2·(-AB·cos ϕ ) co łatwo moŜna przekształcić w: k·AB = AB(1-2cos ϕ ) skąd: cos ϕ = (1-k)/2 Wła ś ciwa o ś symetrii X Działanie wła ś ciwej osi symetrii X na element „R” Projekcja stereograficzna bieguna ś ciany (hkl) przekształcanego wzgl ę dem wła ś ciwej osi symetrii X ϕ= 360o ϕ= 180o ϕ= 120o ϕ= 90o ϕ= 60o
... zobacz całą notatkę






Komentarze użytkowników (0)