To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
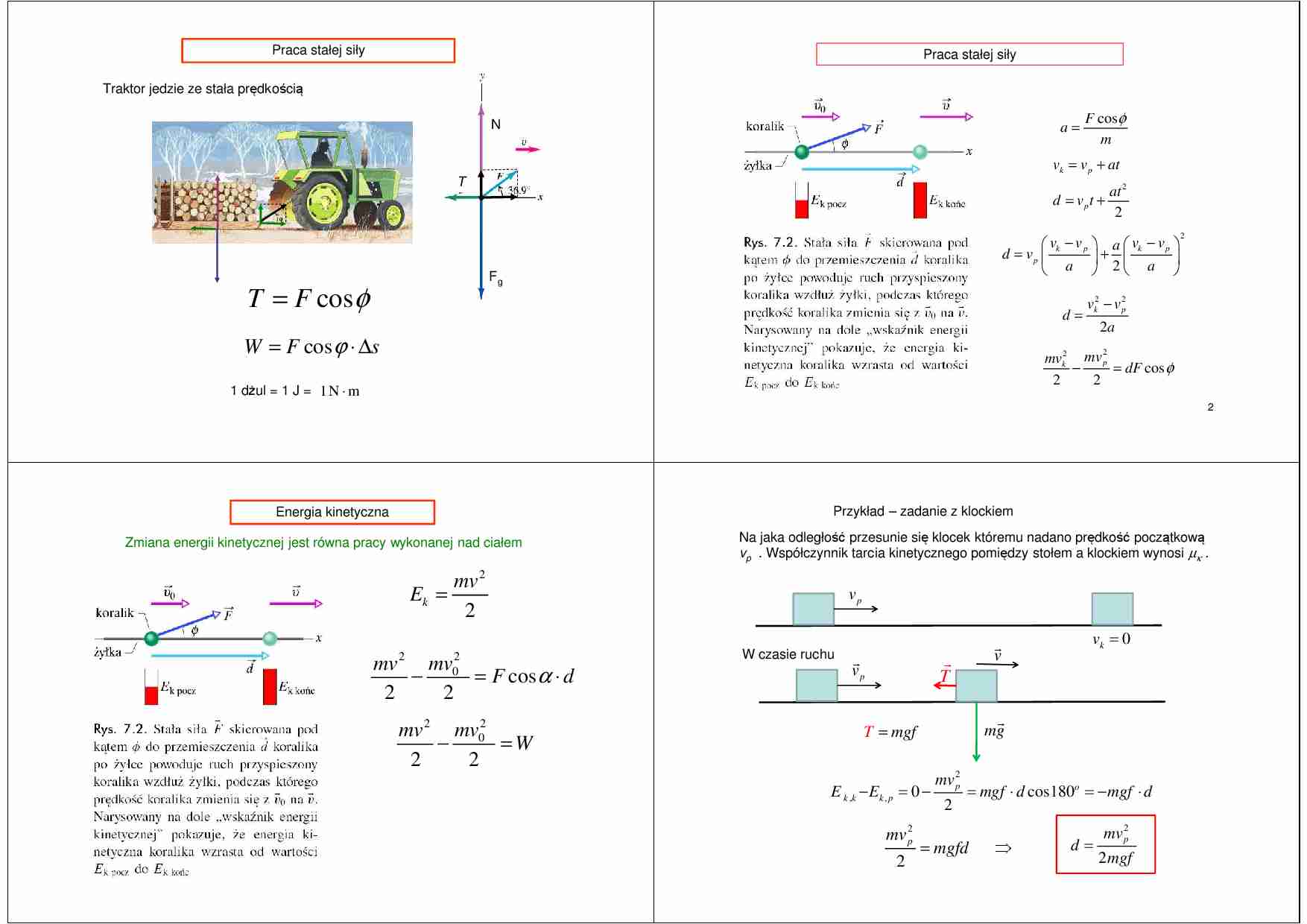


Praca stałej siły
Praca stałej siły
Traktor jedzie ze stała prędkością
a=
N
F cos φ
m
vk = v p + at
T
d = v pt +
v − vp
d = vp k
a
Fg
T = F cos φ
d=
W = F cos ϕ ⋅ ∆s
at 2
2
a vk − v p
+
2 a
2
2
vk − v 2
p
2a
2
2
mvk mv p
−
= dF cos φ
2
2
1 dżul = 1 J = 1 N ⋅ m
2
Przykład – zadanie z klockiem
Energia kinetyczna
Zmiana energii kinetycznej jest równa pracy wykonanej nad ciałem
Ek =
2
Na jaka odległość przesunie się klocek któremu nadano prędkość początkową
vp . Współczynnik tarcia kinetycznego pomiędzy stołem a klockiem wynosi µκ .
mv 2
2
2
0
mv mv
−
= F cos α ⋅ d
2
2
2
mv 2 mv0
−
=W
2
2
vp
W czasie ruchu
v
vp
vk = 0
T
T = mgf
mg
E k ,k − Ek , p = 0 −
mv 2
p
2
mv 2
p
2
= mgf ⋅ d cos180o = −mgf ⋅ d
= mgfd
⇒
d=
mv 2
p
2mgf
Praca siły zmiennej działającej wzdłuż przesunięcia
Praca wykonana przez siłę zewnętrzną
Rozciąganie sprężyny
Fzew = k x
F
x
xp
xk
W = ∑ F ( xi ) ⋅ ∆x
Wzew =
Praca = pole pod krzywą F(x)
kxk + kx p
2
( xk − x p )
1
2
Wzew = k ( xk − x 2 )
p
2
Praca wykonana przez siłę sprężystości
Rozciąganie sprężyny
Fs = − k x
Praca wykonana przez siłę sprężystości
ściskanie sprężyny
Fs = − k x
F
xp
F
xk x
x
xk
xp
F = −k x
Ws = −
kxk + kx p
2
( xk − x p )
1
2
Ws = − k ( xk − x 2 )
p
2
Fzew = kx ⇒
F = −k x
Ws = −
kxk + kx p
2
( xk − x p )
1
2
Ws = − k ( xk − x 2 )
p
2
Wzew = −W
Fzew = kx ⇒
Wzew = −W
Energia potencjalna sprężystości
Rozciąganie sprężyny
Co się stało z pracą wykonaną przez siłę zewnętrzną ?
1
2
Wzew = k ( xk − x 2 )
p
2
E p ( x) =
1
2
Ws = − k ( xk − x 2 )
p
2
Jeżeli Fzew = 0
1 2
kx
2
to :
Wzew = −Ws
E p ( x) + Ek ( x) = E0
Wzew = −Wwewnętrzych
9
Praca siły grawitacji
Energia potencjalna
Podnoszenie do góry
B
g
h
Wg = mg ⋅ d = mgd cos180o = −mgd
d
Energia potencjalna
E p ( y ) ≡ mgy
v0
v0
E (d ) − E (0) = ∆E p
A
E (d ) − E (0) = mgyb − mgya = mgd
Wg = −∆E p
Co się stało z energią kinetyczną jabłka ?
Czyli :
Wg + ∆E p = 0
11
Praca wykonana podczas podnoszenia ciała przez siłę zewnętrzną
Przenoszenie ze stała prędkością
wykonane przez siłę zewnętrzną
b
Siły zachowawcze : niezależność pracy od drogi
Fzew = −mg
E p ( x) + Ek ( x) = E0
Wzew = Fzew ⋅ d = Fzew d ⋅ cos 0o = mgd
d
a
Eb − Ea = mg ( yb − ya ) = mgd
Fzew
Wzew = ∆E p
Wg = −∆E p
Ruch ze stałą prędkością do góry
Wzew = −Wg
Siły zachowawcze
Zastosowanie krzywej energii potencjalnej
W =W
1
ab , 1
a
b
2
E p ( x)
ab .2
Wab + Wba = 0
Praca wykonana przez siłę zachowawczą nie zależy od drogi
E0
Ek ( x)
Całkowita praca wykonana przez siłę zachowawczą po
dowolnej drodze zamkniętej jest równa zeru.
x
położenie
Siły niezachowawcze
Moc
P =
sr
Jednostka :
1 W = 1 J/s
P=
W = mgf ⋅ droga
17
Zasada zachowania energii mechanicznej
W układzie izolowanym, w którym zamiana energii pochodzi jedynie
od sił zachowawczych energia kinetyczna i energia potencjalna
mogą się zmieniać, lecz ich suma czyli energia mechaniczna nie
może ulegać zmianie
... zobacz całą notatkę






Komentarze użytkowników (0)