To tylko jedna z 2 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
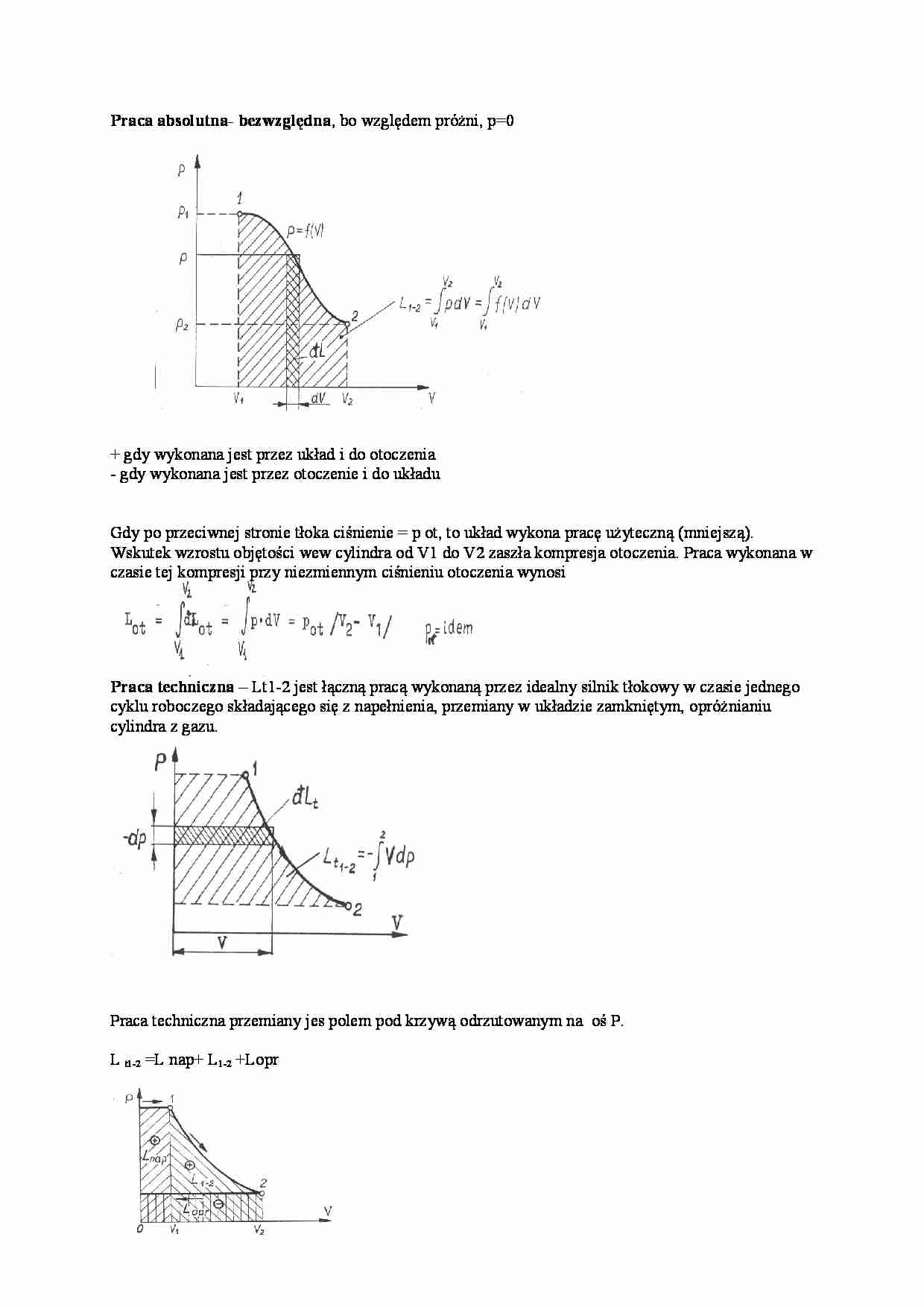

Praca absolutna - bezwzględna
Praca absolutna - bezwzględna, bo względem próżni, p=0 + gdy wykonana jest przez układ i do otoczenia - gdy wykonana jest przez otoczenie i do układu Gdy po przeciwnej stronie tłoka ciśnienie = p ot, to układ wykona pracę użyteczną (mniejszą). Wskutek wzrostu objętości wew cylindra od v1 do v2 zaszła kompresja otoczenia.
Praca wykonana w czasie tej kompresji przy niezmiennym ciśnieniu otoczenia wynosi Praca techniczna – Lt1-2 jest łączną pracą wykonaną przez idealny silnik tłokowy w czasie jednego cyklu roboczego składającego się z napełnienia, przemiany w układzie zamkniętym, opróżnianiu cylindra z gazu. Praca techniczna przemiany jest polem pod krzywą odrzutowanym na oś P. L t1-2 =L nap+ L1-2 +Lopr
II zasada termodynamiki: stwierdza, że w układzie termodynamicznie izolowanym, istnieje funkcja stanu, zwana entropią S, której zmiana ΔS w procesie adiabatycznym spełnia nierówność delta S= 0, przy czym równość zachodzi wtedy i tylko wtedy, gdy proces jest odwracalny. Opiera się na obserwacjach i spostrzeżeniach z życia codziennego-prawo przyrody. Te zasadę formułuje – sformułowanie Kelvina- Plancka „niemożliwe jest zbudowanie silnika, który działając cyklicznie nie wywołałby innych zmian, w układzie i otoczeniu, prócz ochładzania jednego źródła ciepła i wykonania, równoważnej pracy. Czyli niemożliwe jest perpetummobile II rodzaju" Sformułowanie Clausiusa „energia cieplna nie może samorzutnie przenosić się z ciała o niższej temp do ciała o wyższej temp. odwracalność i nieodwracalność procesów def: Odwracalny proces jest gdy po jego odbyciu można biorące w udział składniki układu i otoczenia doprowadzić ponownie do Sanu wyjściowego nie pozostawiając absolutnie żadnych zmian w układzie ani otoczeniu. Proces odwracalny jest granicznym przypadkiem procesu rzeczywistego. Jest to proces idealny w takim sensie jak: ciało idealnie sztywne lub sprężyste, gaz idealny, ciecz idealna.
... zobacz całą notatkę




Komentarze użytkowników (0)