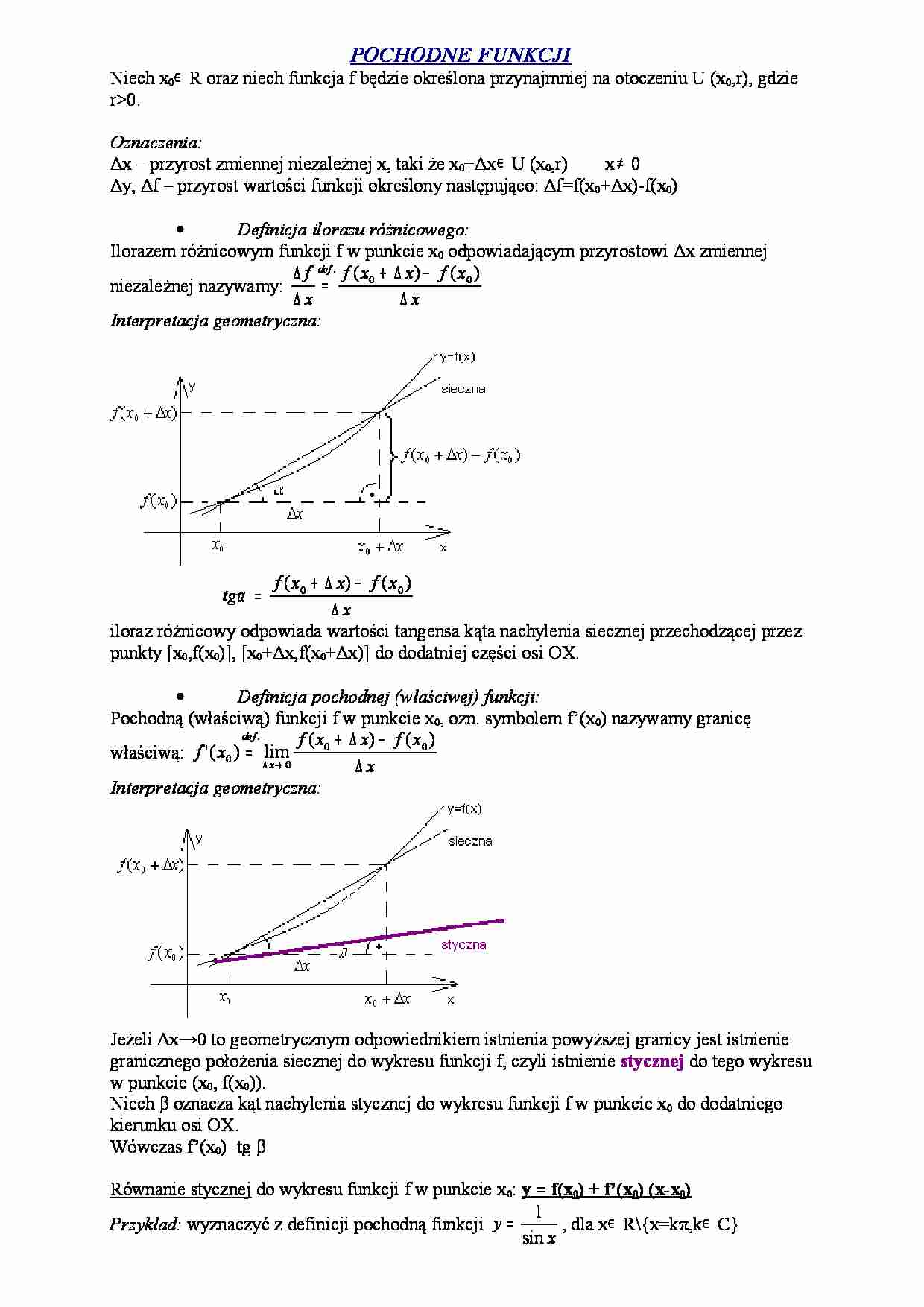
POCHODNE FUNKCJI Niech x0∈ R oraz niech funkcja f będzie określona przynajmniej na otoczeniu U (x0,r), gdzie r0. Oznaczenia: Δx – przyrost zmiennej niezależnej x, taki że x0+Δx∈ U (x0,r) x ≠ 0 Δy, Δf – przyrost wartości funkcji określony następująco: Δf=f(x0+Δx)-f(x0) • Definicja ilorazu różnicowego: Ilorazem różnicowym funkcji f w punkcie x0 odpowiadającym przyrostowi Δx zmiennej niezależnej nazywamy: x x f x x f x f def ∆ − ∆ + = ∆ ∆ ) ( ) ( 0 0 . Interpretacja geometryczna: x x f x x f tg ∆ − ∆ + = ) ( ) ( 0 0 α iloraz różnicowy odpowiada wartości tangensa kąta nachylenia siecznej przechodzącej przez punkty [x0,f(x0)], [x0+Δx,f(x0+Δx)] do dodatniej części osi OX. • Definicja pochodnej (właściwej) funkcji: Pochodną (właściwą) funkcji f w punkcie x0, ozn. symbolem f’(x0) nazywamy granicę właściwą: x x f x x f x f x def ∆ − ∆ + = → ∆ ) ( ) ( lim ) ( ' 0 0 0 . 0 Interpretacja geometryczna: Jeżeli Δx→0 to geometrycznym odpowiednikiem istnienia powyższej granicy jest istnienie granicznego położenia siecznej do wykresu funkcji f, czyli istnienie stycznej do tego wykresu w punkcie (x0, f(x0)). Niech β oznacza kąt nachylenia stycznej do wykresu funkcji f w punkcie x0 do dodatniego kierunku osi OX. Wówczas f’(x0)=tg β Równanie stycznej do wykresu funkcji f w punkcie x0: y = f(x0) + f’(x0) (x-x0) Przykład: wyznaczyć z definicji pochodną funkcji x y sin 1 = , dla x∈ R\{x=kπ,k∈ C} 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 sin cos sin ) sin( 2 2 cos 2 sin lim sin ) sin( 2 cos 2 sin 2 lim sin ) sin( 2 cos 2 sin 2 lim sin ) sin( ) sin( sin lim sin 1 ) sin( 1 lim ) ( ) ( lim ) ( ' x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x f x x f x f x x x x x x − = = ∆ + ⋅ ∆ ∆ + ⋅ ∆ − = ⋅ ∆ + ⋅ ∆ ∆ + ⋅ ∆ − = ⋅ ∆ + ⋅ ∆ ∆ + + ⋅ ∆ − − = = ⋅ ∆ + ⋅ ∆ ∆ + − = ∆ − ∆ + = ∆ − ∆ + = → ∆ → ∆ → ∆ → ∆ → ∆ → ∆ • Definicja pochodnych jednostronnych funkcji: Niech f będzie określona przynajmniej na lewostronnym otoczeniu U_(x0) [prawostronnym
(…)
… ma pochodną na otoczeniu U(x0), funkcja f” jest ciągła w punkcie x0 oraz
punkt P0[x0, f(x0)] jest punktem przegięcia krzywej y=f(x), to f”(x0)=0.
Przykład na to, że nie jest to warunek wystarczający:
y=x4, x ∈ R
y’=4x3
y”=12x2
warunek konieczny ⇔ y”(x)=0 ⇒ x=0,
ale funkcja nie posiada w tym
punkcie punktu przegięcia.
•
Twierdzenie: I warunek wystarczający istnienia punktu przegięcia:
Niech x0 ∈ R oraz niech funkcja f będzie określona przynajmniej na otoczeniu U(x0) tego
punktu. Niech ponadto funkcja f ma w punkcie x0 pochodną właściwą lub niewłaściwą.
Wówczas jeżeli: δ ∨> 0 f " ( x) < 0 dla każdego x ∈ S_(x0,δ)
i δ ∨> 0 f " ( x) > 0 dla każdego S+(x0,δ)
lub na odwrót, to [x0, f(x0)] jest punktem przegięcia wykresu tej funkcji.
•
Twierdzenie: II warunek wystarczający istnienia punktu przegięcia:
Niech x0 ∈ R…
… ( x) − g ' ( x) ⋅ f ( x)
, o ile g ( x) ≠ 0
g ( x) ' =
[ g ( x)]2
,
L' M − M ' L
L
=
M2
M
Wzory te są właściwe dla
pochodnych jednostronnych jeśli
nie występują symbole
nieoznaczone.
•
Twierdzenie o pochodnej funkcji złożonej:
Jeżeli:
1. Funkcja h ma pochodną w punkcie x
2. Funkcja f ma pochodną w punkcie y=h(x)
to funkcja złożona f h ma w punkcie x pochodną:
[ ( f h ) ( x…
… (b) − f (a )
na przedziale otwartym (a,b), to istnieje taki punkt c ∈ (a,b), że f ' (c ) =
.
b− a
Interpretacja geometryczna:
MONOTONICZNOŚĆ FUNKCJI
•
Twierdzenie: warunki wystarczające monotoniczności funkcji:
⊂ R oznacza przedział (skończony lub nieskończony). Jeżeli dla każdego x ∈ I:
Niech I
1) f’(x)=0, to funkcja f jest stała na przedziale I
2) f’(x)>0, to funkcja f jest rosnąca na przedziale…
…’(x0)=0, to punkt x0 nazywa się punktem stacjonarnym funkcji f.
UWAGA: Warunek f’(x0)=0 jest warunkiem koniecznym na to, aby funkcja f posiadająca
pochodną w punkcie x0, miała w tym punkcie ekstremum, ale nie jest warunkiem
wystarczającym.
Przykład: Niech y=x3, D:R
y’=3x2
Warunek konieczny istnienia ekstremum ⇔ 3x2=0
x=0
Warunek konieczny jest spełniony, ale funkcja nie posiada
ekstremum w x0=0…
…) nie istnieje
•
Twierdzenie: związek między ciągłością a istnieniem pochodnej:
Jeżeli funkcja ma pochodną właściwą w punkcie, to jest ciągła w tym punkcie.
UWAGA: Ale nie na odwrót!!! Tzn. z ciągłości funkcji nie wynika istnienie pochodnej.
Przykład: y=│x│ jest funkcją ciągłą, ale nie ma pochodnej w x0=0!!!
•
Definicja pochodnej funkcji na zbiorze:
Funkcja ma pochodną właściwą na zbiorze ⇔ , gdy ma pochodną…
…).
•
Definicja pochodnej niewłaściwej funkcji:
Niech f będzie funkcją ciągłą w punkcie x0 ∈ R. funkcja f ma w punkcie x0 pochodną
f ( x0 + ∆ x ) − f ( x0 )
f ( x0 + ∆ x ) − f ( x0 )
= + ∞ lub lim
= − ∞ co
niewłaściwą , gdy: lim
∆ x→ 0
∆ x→ 0
∆x
∆x
zapisujemy: f’(x0)=+∞ lub f’(x0)=-∞.
y=f(x)
UWAGA: Jeżeli funkcja f posiada w punkcie x0
pochodną niewłaściwą, to równanie stycznej do wykresu
funkcji y=f(x…
… ∆ x − 0
sin 5 ∆ x
1
f ' (0) = lim
= lim
= lim
= + = +∞ ⇒
x= 0
∆ x→ 0
∆ x→ 0
∆ x→ 0 5
∆x
∆x
asymptota
∆ x ⋅ 5 (∆ x) 4 0
pionowa
POCHODNE FUNKCJI ELEMENTARNYCH:
(c' ) = 0, c ∈ R
( x n ) = nx n− 1 , n ∈ R
( a x ) = a x ln a, a > 0, a ≠ 1
∆x
a − 1 = t ∧ ∆ x → 0 ⇒ t → 0
∆x
a = t+ 1
x+ ∆ x
x
x
∆x
x
∆x
a
− a
a ⋅a − a
a −1
dowód : f ' ( x ) = lim
= lim
= lim a x
= ln a ∆ x…
... zobacz całą notatkę





Komentarze użytkowników (0)