To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
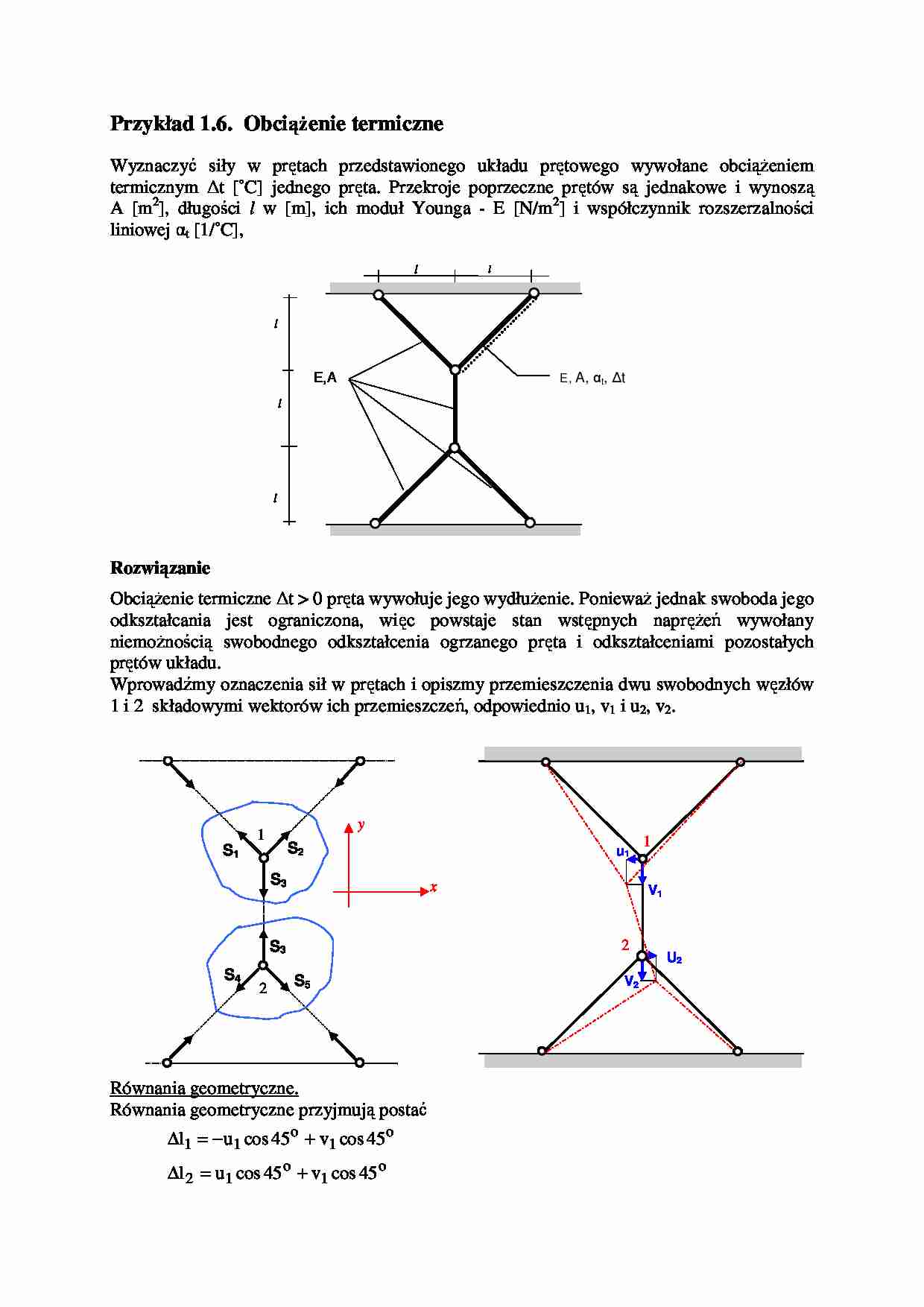


Przykład 1.6. ObciąŜenie termiczne
Wyznaczyć siły w prętach przedstawionego układu prętowego wywołane obciąŜeniem
termicznym ∆t [˚C] jednego pręta. Przekroje poprzeczne prętów są jednakowe i wynoszą
A [m2], długości l w [m], ich moduł Younga - E [N/m2] i współczynnik rozszerzalności
liniowej αt [1/˚C],
l
l
l
E, A, αt, ∆t
E,A
l
l
Rozwiązanie
ObciąŜenie termiczne ∆t 0 pręta wywołuje jego wydłuŜenie. PoniewaŜ jednak swoboda jego
odkształcania jest ograniczona, więc powstaje stan wstępnych napręŜeń wywołany
niemoŜnością swobodnego odkształcenia ogrzanego pręta i odkształceniami pozostałych
prętów układu.
Wprowadźmy oznaczenia sił w prętach i opiszmy przemieszczenia dwu swobodnych węzłów
1 i 2 składowymi wektorów ich przemieszczeń, odpowiednio u1, v1 i u2, v2.
y
1
S2
S1
S3
x
2
S5
Równania geometryczne.
Równania geometryczne przyjmują postać
∆l1 = − u1 cos 45 o + v1 cos 45 o
∆l 2 = u1 cos 45 o + v1 cos 45 o
1
V1
2
S3
S4
u1
V2
U2
∆l 3 = − v1 + v 2
∆l 4 = u 2 cos 45 o − v 2 cos 45 o
(1-5)
∆l 5 = − u 2 cos 45 o − v 2 cos 45 o
Warunki fizyczne
WydłuŜenia prętów wynoszą:
S 2l
∆l1 = 1
,
EA
S 2l
∆l 4 = 4
,
EA
∆l 2 =
S 2 2l
EA
S 2l
∆l 5 = 5
EA
+ 2α t ∆tl
,
S l
∆l 3 = 3 ,
EA
(6-10)
Wyznaczając siły z równań (6-10) i uwzględniając równania (1-4) otrzymujemy
EA
S1 =
(− u1 + v1 )
2l
EA
S2 =
(u1 + v1 − 2α t ∆tl)
2l
EA
S3 =
(− v1 + v 2 )
(6*-10*)
l
EA
S4 =
(u 2 − v 2 )
2l
EA
S5 =
(− u 2 − v 2 )
2l
Zapiszemy teraz równania równowagi dla węzłów swobodnych 1 i 2.
Węzeł 1
1
1
+ S2
=0
2
2
1
1
+ S2
− S3 = 0
∑ Piy = 0 ⇒ S1
2
2
∑ Pix = 0 ⇒ −S1
(11,12)
Węzeł 2
1
1
+ S5
=0
2
2
1
1
− S5
+ S3 = 0
∑ Piy = 0 ⇒ −S 4
2
2
∑ Pix = 0 ⇒ −S 4
(13,14)
Podstawiając wyraŜenia (6*-10*) do równań (11-14) mamy układ 4 równań:
EA
−
(− u1 + v1 ) + EA (u1 + v1 − 2α t ∆tl) = 0
2l
2l
EA
EA
(− u1 + v1 ) + (u1 + v1 − 2α t ∆tl) − 2 EA (− v1 + v 2 ) = 0
2l
2l
l
EA
−
(u 2 − v 2 ) + EA (− u 2 − v 2 ) = 0
2l
2l
EA
−
(u 2 − v 2 ) − EA (− u 2 − v 2 ) + 2 EA (− v1 + v 2 ) = 0
2l
2l
l
który po uporządkowaniu ma postać:
2
u1 − α t ∆tl = 0
(2 + 2 2 )v1 − 2v2 =
u2 = 0
(
2α t ∆tl
)
2 v1 − 2 + 2 v 2 = 0
Z rozwiązania układu otrzymujemy
u1 = α t ∆tl ,
u2 = 0 ,
3+ 2
v1 =
α t ∆tl ,
7
4− 2
v2 =
α t ∆tl .
7
Z równań (6*-10*) wyznaczamy siły w prętach
1
S1 = S 2 = S 4 = S5 = −
4 − 2 EAα t ∆t = −0.1847 ⋅ EAα t ∆t ,
14
1
S3 = − 2 2 − 1 EAα t ∆t = −0.2612 ⋅ EAα t ∆t .
7
(
(
)
)
Wszystkie pręty są ściskane.
Ćwiczenie
Wykorzystując przedstawione rozwiązanie wyznacz siły w prętach tego układu, przy
załoŜeniu, Ŝe pręt nr 2 jest nieodkształcalny (np. wykonany jest z materiału o duŜo większym
module Younga, niŜ pozostałe pręty). Porównaj rozwiązania.
E, A, αt, ∆t
E,A
E1 A
E1A→∞
3
... zobacz całą notatkę






Komentarze użytkowników (0)