To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
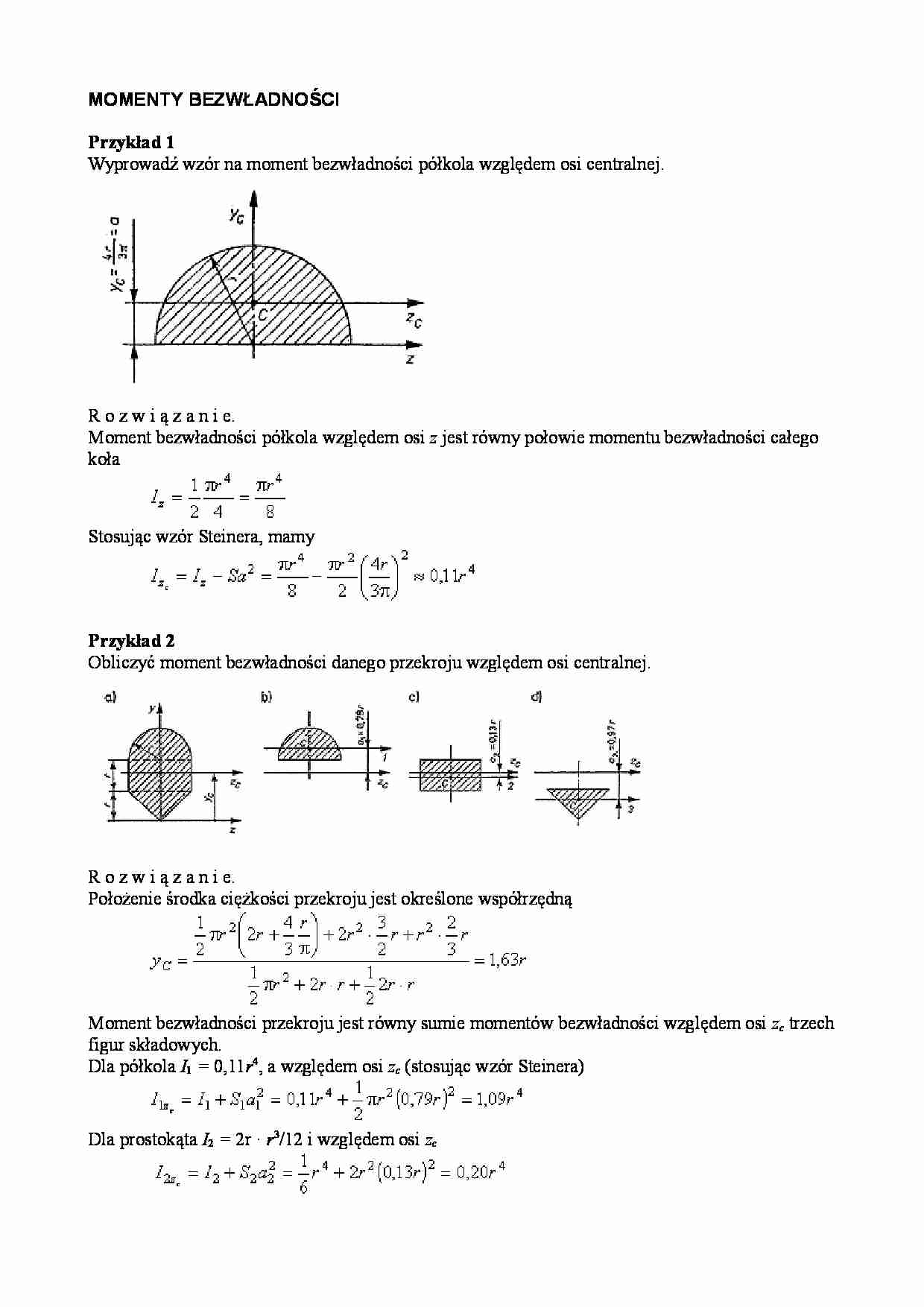


MOMENTY BEZWŁADNOŚCI Przykład 1 Wyprowadź wzór na moment bezwładności półkola względem osi centralnej. R o z w i ą z a n i e. Moment bezwładności półkola względem osi z jest równy połowie momentu bezwładności całego koła Stosując wzór Steinera, mamy Przykład 2 Obliczyć moment bezwładności danego przekroju względem osi centralnej. R o z w i ą z a n i e. Położenie środka ciężkości przekroju jest określone współrzędną Moment bezwładności przekroju jest równy sumie momentów bezwładności względem osi zc trzech figur składowych. Dla półkola I 1 = 0,11 r 4, a względem osi zc (stosując wzór Steinera) Dla prostokąta I 2 = 2r · r 3/12 i względem osi zc a dla trójkąta I 3 = 2r · r 3/36, zatem Ostatecznie otrzymamy Przykład 3 Obliczyć odśrodkowy moment bezwładności ćwiartki koła względem układu osi yz . R o z w i ą z a n i e. Elementarne pole wynosi a współrzędna jego środka ciężkości Moment odśrodkowy wynosi Przykład 4 Wyznacz moment bezwładności cienkiego jednorodnego pręta o masie m i długości l względem osi Ox i osi centralnej Cxc . R o z w i ą z a n i e. Wycinamy myślowo w odległości y od osi Ox element długości d y . Masa elementu o długości d y wynosi Pomijając wymiary poprzeczne pręta ( z = 0) otrzymujemy Moment bezwładności względem osi centralnej Cxc . Przykład 5 Wyznaczyć momenty bezwładności płaskiej kołowej płytki o masie m i promieniu r względem osi Ox , Oy i Oz . R o z w i ą z a n i e. Moment bezwładności względem osi Oz jest biegunowym momentem bezwładności. W odległości od środka tarczy wycinamy pierścień o grubości d , zatem Masa wyciętego pierścienia wynosi Stąd Mamy także Stąd Możemy również napisać Zatem Document Outline MOMENTY BEZWŁADNOŚCI
... zobacz całą notatkę






Komentarze użytkowników (0)