Metody i algorytmy optymalizacji dr Helena Spyra Wykład 7
Ekstremum warunkowe
Przykład
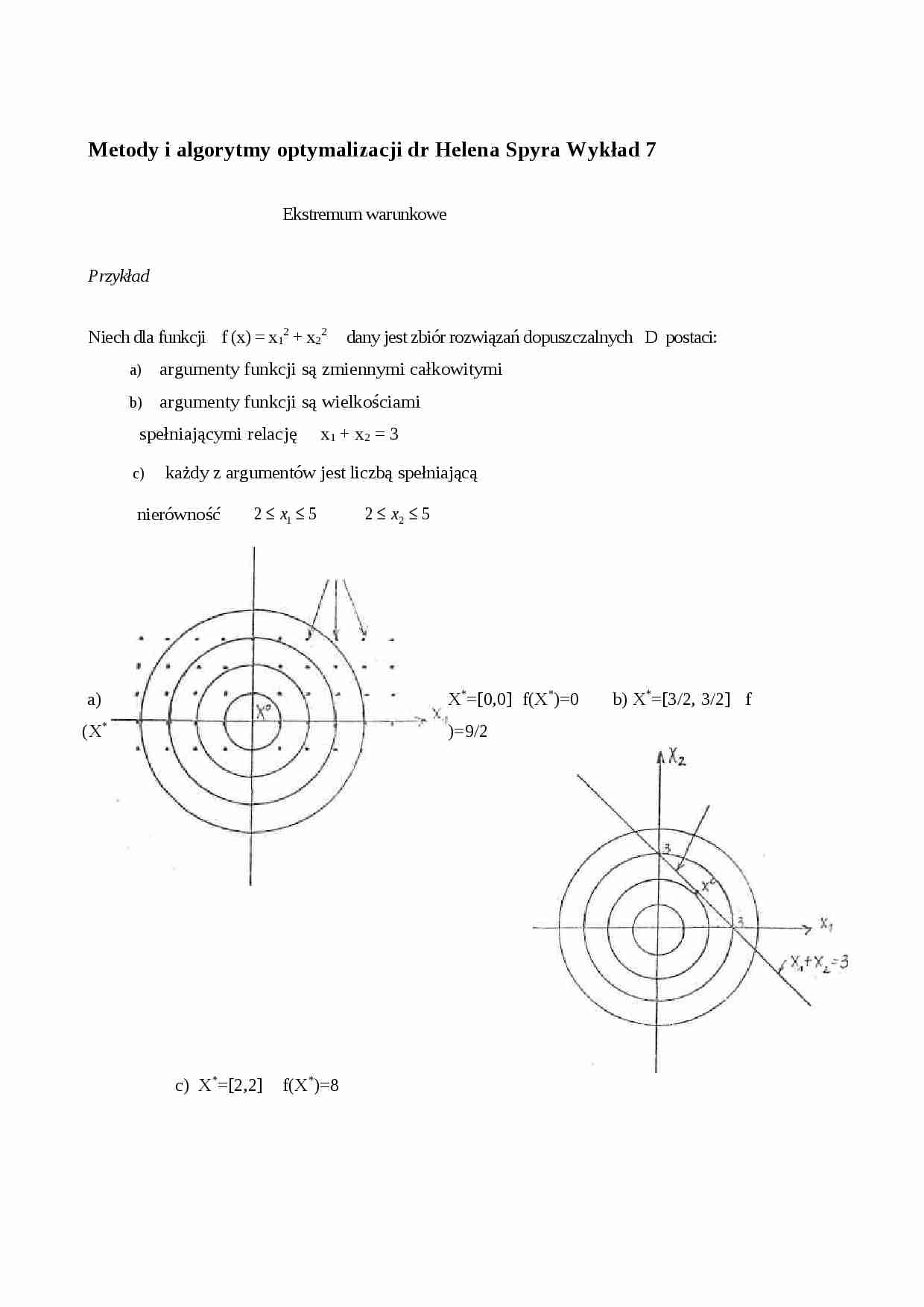
Niech dla funkcji f (x) = x12 + x22 dany jest zbiór rozwiązań dopuszczalnych D postaci:
argumenty funkcji są zmiennymi całkowitymi
argumenty funkcji są wielkościami
spełniającymi relację x1 + x2 = 3
każdy z argumentów jest liczbą spełniającą nierówność a) X*=[0,0] f(X*)=0 b) X*=[3/2, 3/2] f (X*)=9/2 c) X*=[2,2] f(X*)=8
Przyklad
f(x) = x12 + x22 przy czym x € R2 warunek ograniczający g(x)=x1+x2-2=0
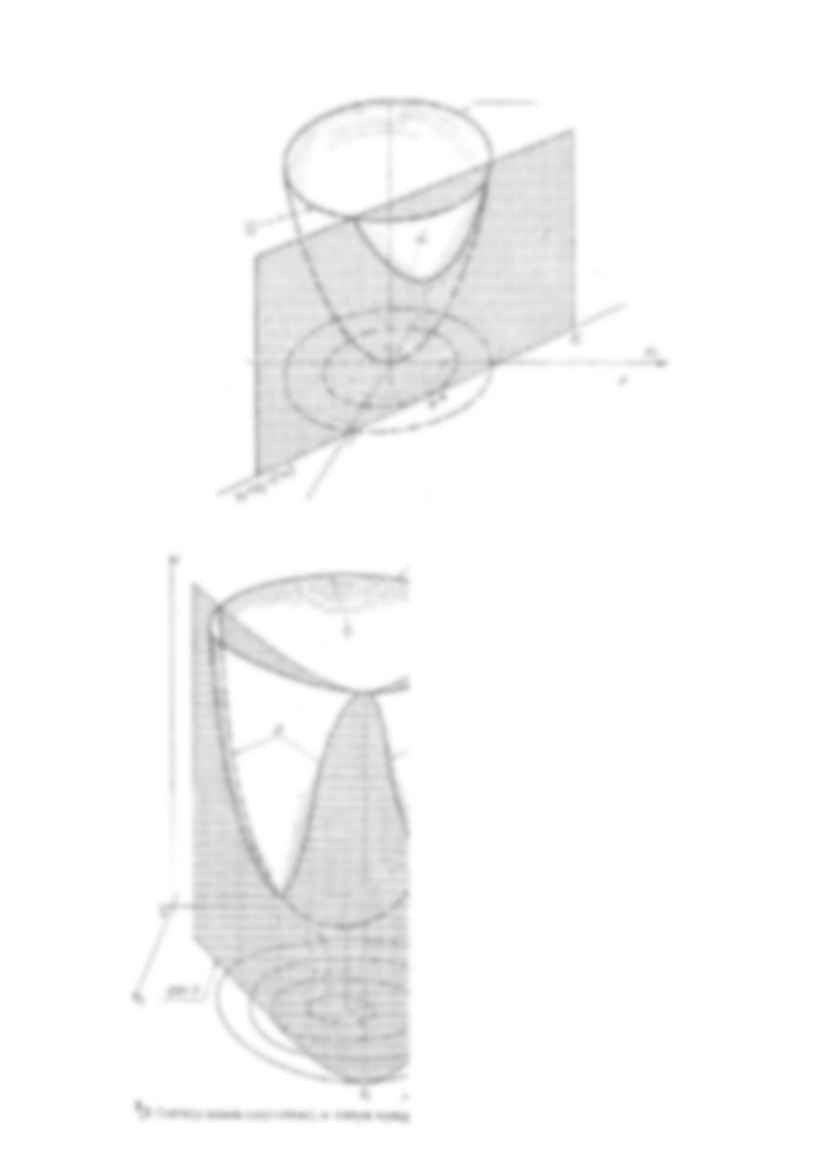
Funkcja kryterialna ma minimum bezwarunkowe w punkcie (0,0) (nie należy do zbioru punktów dopuszczalnych ) Przykład (rys)
g(x)=0 powierzchnia będąca pobocznicą walca parabolicznego; w punkcie x1 istnieje globalne minimum warunkowe, w punkcie x3 lokalne;
w punkcie x2 istnieje maksimum warunkowe, globalne. Zadanie ekstremum warunkowego
f (X)→extr (min lub max) przy warunku X € D,
D = {X: X€Rn gi(X) ≤ ai , i € ln , hi(X)= bi , i € lr , X€S }
Funkcje gi(X), i € In , hi(X), i € Ir są funkcjami rzeczywistymi, zbiór S € Rn jest pewnym zbiorem przestrzeni Rn określonym np. za pomocą funkcji zdaniowej Klasyczne zadania programowania matematycznego
f (X) → min
przy warunkach
hi(X) = bi i € Ir = { i,…,p} p ≤ n
funkcje f (X), hi(X) są funkcjami klasy C1 Niech punkt X* jest rozwiązaniem optymalnym zadania. Zakładamy, że w punkcie X* rząd jakobianu układu funkcji h1(X) ,…,hp(X) jest równy p , co oznacza, że w punkcie X* gradienty funkcji h1(X),…, hp(X) są liniowo niezależne; w jakobianie
(2*
podmacierz składająca się z p ostatnich kolumn ma wyznacznik różny od zera. wektor X1 n-p składowych
X2 p składowych
Przyjmijmy, że k(X1) jest pewną funkcją wektorową,
k: En-p → Ep o składowych k
(…)
… w pewnym punkcie (X*, U*):
W punkcie będącym rozwiązaniem optymalnym zadania gradient funkcji kryterium można przedstawić jako pewną kombinację liniową gradientów funkcji wyznaczających zbiór rozwiązań optymalnych. Gdy funkcje f (X) i hi(X) i=1,…,p są klasy C2 to hesjan funkcji Lagrange'a ze względu na wektor X
ma postać:
Twierdzenie
Jeżeli punkt X* jest rozwiązaniem optymalnym zadania programowania…
…(X) = x1 - x2 + x3 - 7 = 0
warunki konieczne istnienia ekstremum warunkowego :
x1*= 2, x2*= 3, x3*= 2 oraz z warunków dostatecznych - punkt x* jest szukanym rozwiązaniem.
Interpretacja mnożników Lagrange'a w zadaniu f (x) → min
przy warunkach hi(X) = bi i = 1,…,p
wielkości bi są zmiennymi ; przy zmianie wielkości bi zmienia się również rozwiązanie X* , które możemy traktować jako funkcje zmiennych…
…*) < 0
Zawsze uj*≥ 0 j=1,2,3
- jeżeli gj(x*) < 0 to zawsze uj*= 0
- jeżeli gj(x*) = 0 to może być uj*= 0
- jeżeli uj*> 0 to zawsze gj(x*)= 0
Jeżeli warunek ograniczający w punkcie x* nie jest aktywny, czyli gj(x*) < 0, to odpowiadający mu mnożnik Lagrange'a uj* jest równy zeru. Jeżeli mnożnik ten jest dodatni, to w punkcie x* warunek ograniczający jest aktywny gj(x*) = 0 …
... zobacz całą notatkę




Komentarze użytkowników (0)