Metody aktuarialne podstawy z rachunku prawdopodobieństwa

Nasza ocena:

3
Pobrań: 77
Wyświetleń: 700
Komentarze: 0
Notatek.pl

Pobierz ten dokument za darmo

Pobierz notatkę
Podgląd dokumentu
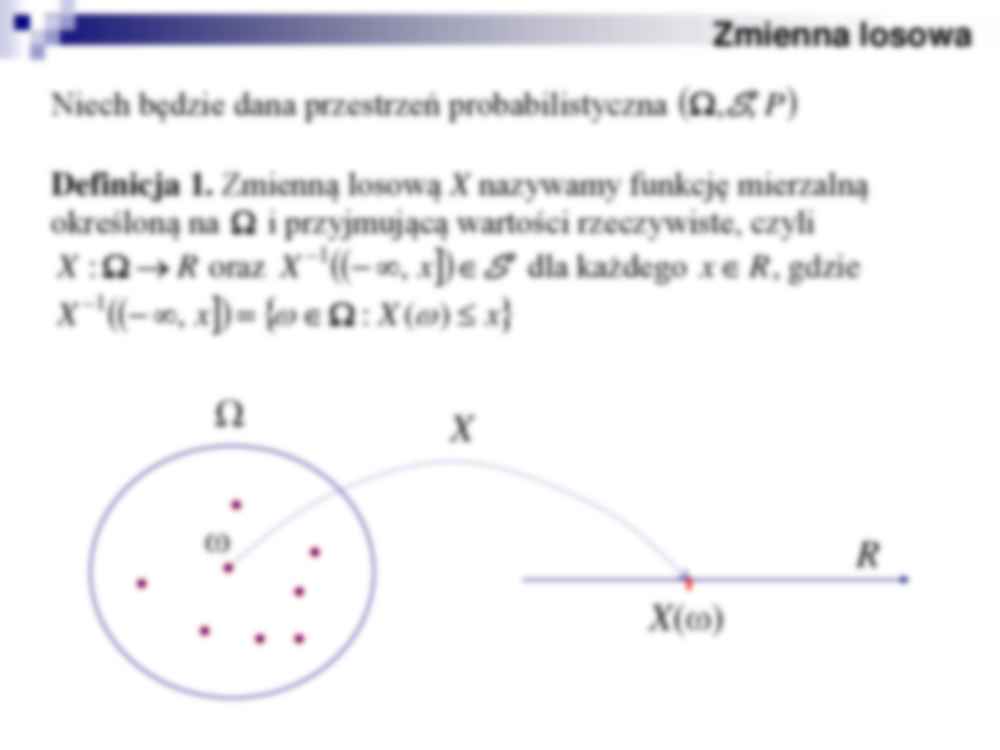
Metody aktuarialne podstawy z rachunku prawdopodobieństwa - strona 1 Metody aktuarialne podstawy z rachunku prawdopodobieństwa - strona 2 Metody aktuarialne podstawy z rachunku prawdopodobieństwa - strona 3

Fragment notatki:

Metody aktuarialne  Podstawy z rachunku prawdopodobieństwa  Zmienna losowa  Niech będzie dana przestrzeń probabilistyczna    P S, ,      Definicja 1.  Zmienną losową  X  nazywamy funkcję mierzalną  określoną na   i przyjmującą wartości rzeczywiste, czyli  R X   :  oraz      S     x X , 1  dla każdego  R x   , gdzie        x X x X       ) ( : , 1        Ω  ω  X (ω)  R                  X  Zmienna losowa  Definicja 1.  Zmienną losową  X  nazywamy funkcję mierzalną  określoną na   i przyjmującą wartości rzeczywiste, czyli  R X   :  oraz      S     x X , 1  dla każdego  R x   , gdzie        x X x X       ) ( : , 1        Ω  x  R                  x 1    x2     x3        x4        x ,           x X x X       ) ( : , 1    Zmienna losowa  Definicja 2.  Dystrybuantą zmiennej losowej  X   nazywamy funkcję   F  , która każdej liczbie rzeczywistej  przyporządkowuje prawdopodobieństwo, że zmienna ta  przyjmuje wartości mniejsze lub równe tej liczbie, czyli:       1 , 0 :  R F               x X P x X P x F , ) ( 1         Zmienna losowa  Własności dystrybuanty:  1.  1 ) ( 0   x F .  2.  F  jest funkcją niemalejącą (stałą lub rosnącą).  3.  F  jest funkcją prawostronnie ciągłą, tzn.      ) ( ) ( lim 0 x F x x F x         4.    0 ) ( lim       x F F x  oraz    1 ) ( lim      x F F x    Zmienna losowa  W dalszym ciągu symbolem     x F  będziemy oznaczać  lewostronną granicę dystrybuanty w punkcie  x , czyli:      ) ( lim ) ( 0 x x F x F x          Uwaga !      x X P x x F x F x        ) ( lim ) ( 0     Można udowodnić następujące równości:  1.    ) ( ) ( a F b F b X a P      

(…)

…
- dla zmiennej losowej ciągłej:


m

0
m
E ( X  m)r   x r f ( x)dx  mr  f ( x)dx
Własności:
1. Jeżeli zmienna przyjmuje wartości nieujemne to
istnieją wszystkie ograniczone moment rzędu r  0 .
2. lim E  X  m  E ( X ) , jeżeli wartość oczekiwana
m 
istnieje
Funkcja tworząca
Niech
X będzie zmienną losową przyjmującą
nieujemne wartości całkowite. Funkcję tworzącą h X
rozkładu zmiennej losowej X definiujemy następująco:
    P X  xi s
hX ( s )  E s
X
i
xi
 pi s ,  1  s  1
xi
i
Przykład
Zmienna losowa X ma rozkład
xi
0
1
2
3
pi
1/8
3/8
3/8
1/8
Funkcja tworząca ma postać:
1 3 1 3 2 1 3
hX ( s )   s  s  s
8 8
8
8
 Funkcja tworząca (generująca) momenty
Funkcją tworzącą momenty (w skrócie ftm) rozkładu
zmiennej losowej X o dystrybuancie F nazywamy funkcję
M X określoną następująco:
 

M X ( s)  E e sX   e sx dF ( x) .

Dziedziną tej funkcji jest przedział, w którym całka
występująca po prawej stronie jest zbieżna.
Jej nazwa związana jest z równością:
 
(
r  E X r  M Xr ) (0), r  1,2,3,...,
z której wynika, że w przypadku, gdy znamy funkcję
tworzącą momenty rozkładu zmiennej losowej X, możemy
wyznaczyć jej momenty zwykłe rzędu r, obliczając r-te
pochodne funkcji M X…
… ( X )  
Odchyleniem standardowym będziemy
nazywać liczbę:
  Var (X ) .
 Momenty zwykłe
Momentem zwykłym rzędu r nazywamy liczbę:
 

r  E X r   x r dF (x) ,

o ile, całka ta jest skończona. Rząd r może być równy
r=0,1,2,... .
W szczególnym przypadku:
0  1, 1    E ( X ) .
Momenty centralne
Załóżmy, że istnieje skończona wartość oczekiwana E(X).
Jeżeli ponad to, odpowiednia całka…
... zobacz całą notatkę



Komentarze użytkowników (0)

Zaloguj się, aby dodać komentarz