To tylko jedna z 28 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
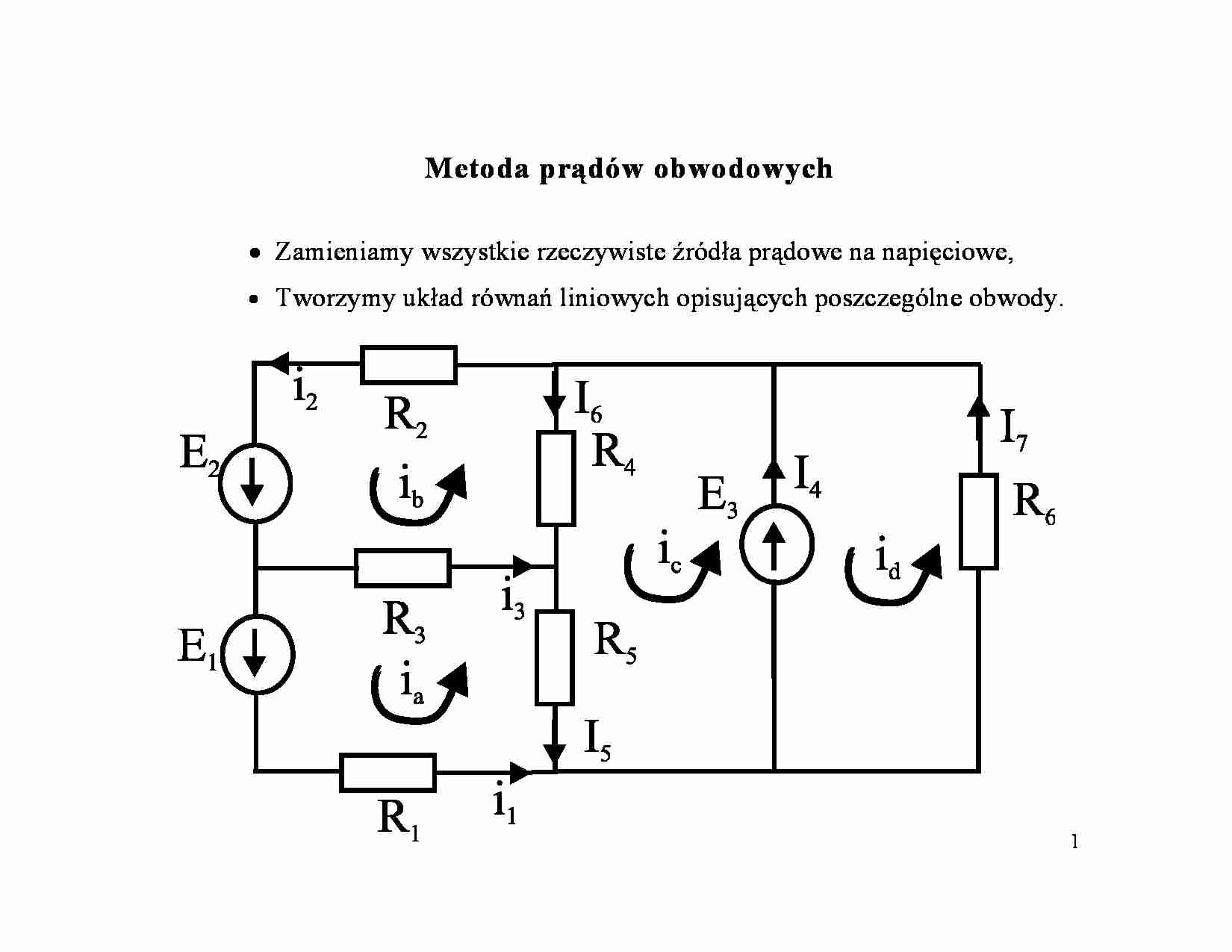


1 Metoda prądów obwodowych · Zamieniamy wszystkie rzeczywiste źródła prądowe na napięciowe, · Tworzymy układ równań liniowych opisujących poszczególne obwody. 2 Dowolną sieć liniową składającą się z elementów skupionych można opisać za pomocą układu i równań liniowych 1 + - = w g i gdzie: g – liczba gałęzi sieci, w – liczba niezależnych węzłów. ï ï ï þ ï ï ï ý ü - = + = + - = - - = 6 7 3 4 6 5 5 3 2 2 4 6 3 3 2 3 3 5 5 1 1 1 R i E ) d R i R i E ) c R i R i R i E ) b R i R i R i E ) a 3 Prądy gałęziowe można zastąpić prądami obwodowymi: ia, ib, ic oraz id ( ) ( ) ( ) ( ) ( ) ( ) ï ï ï þ ï ï ï ý ü - = - + - = + - - - = - - - - = 6 3 4 5 3 2 4 3 2 3 5 1 1 R i E ) d R i i R i i E ) c R i R i i R i i E ) b R i i R i i R i E ) a d b c a c b b c a b a b a c a 6 3 7 R E d i i - = = 4 Pozostaje do rozwiązania układ trzech równań, który można przekształcić do postaci ( ) ( ) ( ) ï ï þ ï ï ý ü + + - - = - + + + - = - - + + = c b a c b a c b a i R R i R i R E ) c i R i R R R i R E ) b i R i R i R R R E ) a 5 4 4 5 3 4 4 3 2 3 2 5 3 5 3 1 1 ï þ ï ý ü + - - = - + - = - - = c cc b cb a ca c c bc b bb a ba b c ac b ab a aa a i R i R i R E i R i R i R E i R i R i R E i - równań 5 Zależność tę można zapisać w postaci równania macierzowego [ ] [ ] [ ] 1 1 , i c i, i c , i c i R E = gdzie: [Ec] – wektor obwodowych sił elektromotorycznych, [Rc] – macierz rezystancji obwodowych, [ic] – wektor prądów obwodowych. Metoda Cramera: Liczymy wyznacznik główny Wcc macierzy rezystancji obwodowych, z zależności cc cb ca bc bb ba ac ab aa cc R R R R R R R R R W - - - - - - = 6 · Liczymy wyznaczniki pomocnicze: cc cb c bc bb b ac ab a a R R E R R E R R E W - - - - = cc c ca bc b ba ac a aa b R E R R E R R E R W - - - - = c cb ca b bb ba a ab aa c E R
(…)
… ) 1u1 + 1u2 + 1u3 + 0u4 + 0u5 + 0u6 = 0
c2 ) 0u1 - 1u2 + 0u3 - 1u4 - 1u5 + 0u6 = 0
c3 ) 0u1 + 0u2 - 1u3 + 0u4 + 1u5 + 1u6 = 0
ü
ï
ý
ï
þ
z tego układu równań otrzymujemy drugie prawo Kirchhoffa w postaci
uogólnionej
gdzie :
[d]i ,k [u g ]k ,1 = [0]i ,k
[ug] – wektor napięć gałęziowych,
[d] – macierz gałęziowo obwodowa (obwodowa).
15
Macierz [d] dla rozpatrywanego obwodu ma postać
0 0 0ù
é1 1 1
ê0 - 1 0…
… krawędzi.
G = á X ,Y , I ñ
14
· Określenie macierzy strukturalnej [d]
c1 ) 1u1 + 1u2 + 1u3 + 0u4 + 0u5 + 0u6 = 0 ü
ï
c2 ) 0u1 - 1u2 + 0u3 - 1u4 - 1u5 + 0u6 = 0 ý
c3 ) 0u1 + 0u2 - 1u3 + 0u4 + 1u5 + 1u6 = 0 ï
þ
z tego układu równań otrzymujemy drugie prawo Kirchhoffa w postaci
uogólnionej
[d]i ,k [u g ]k ,1 = [0]i ,k
gdzie : [ug] – wektor napięć gałęziowych,
[d] – macierz gałęziowo obwodowa (obwodowa).
15…
… obwodowe z zależności:
Wa
Wb
Wc
ia =
, ib =
, ic =
Wcc
Wcc
Wcc
· Liczymy prądy gałęziowe z zależności:
i1 = ia,
i2 = ib,
i3 = ib - ia,
i4 = ic - id,
i5 = ic - ia,
i6 = ic - ib,
i7 = id.
7
Metoda potencjałów węzłowych
W metodzie tej:
· zamieniamy wszystkie rzeczywiste źródła napięciowe na źródła prądowe,
· wybieramy węzeł odniesienia,
zapisujemy w = w’ – 1 liniowych równań węzłowych dla pozostałych węzłów…
... zobacz całą notatkę






Komentarze użytkowników (0)