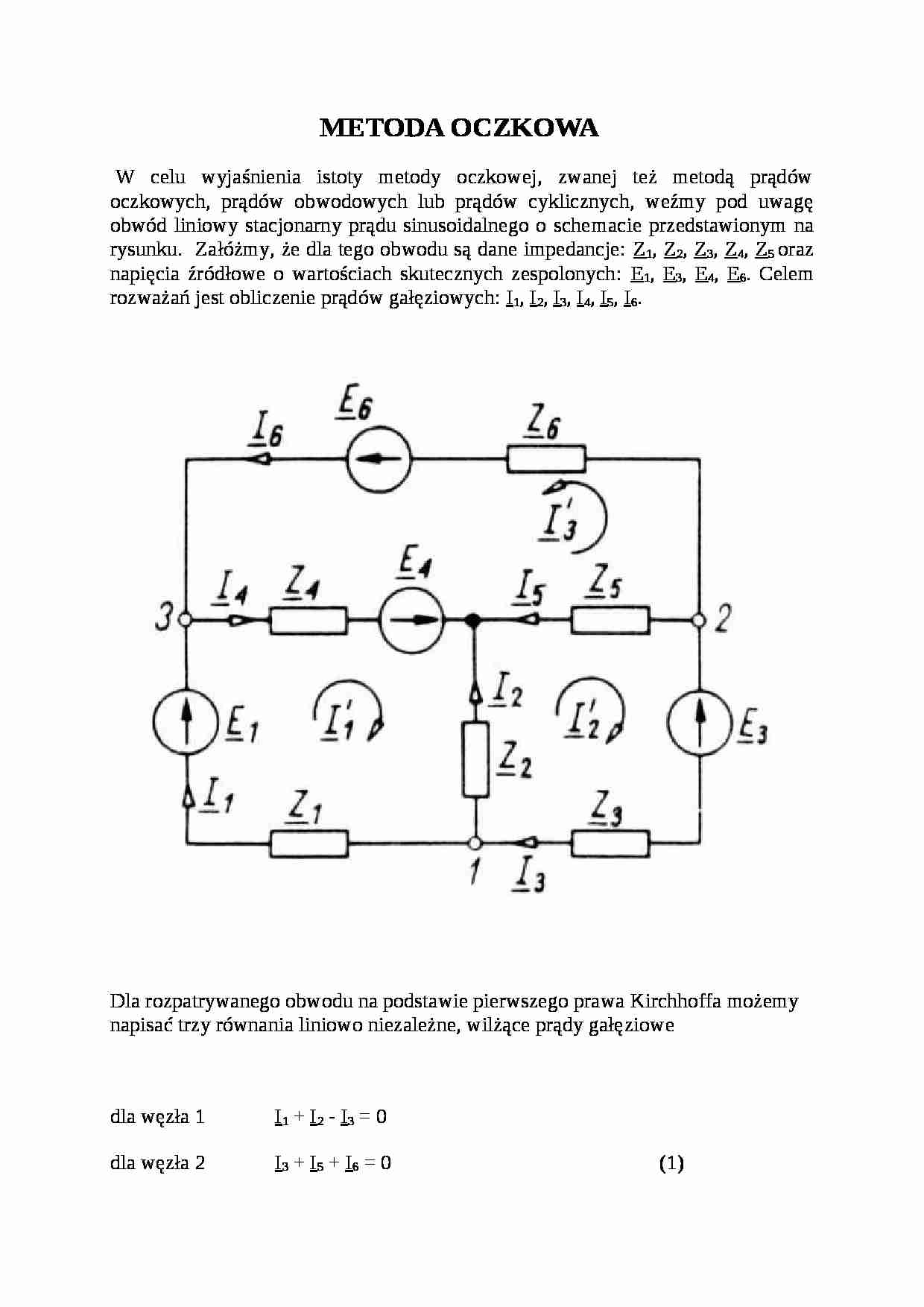
METODA OCZKOWA W celu wyjaśnienia istoty metody oczkowej, zwanej też metodą prądów oczkowych, prądów obwodowych lub prądów cyklicznych, weźmy pod uwagę obwód liniowy stacjonarny prądu sinusoidalnego o schemacie przedstawionym na rysunku. Załóżmy, że dla tego obwodu są dane impedancje: Z1, Z2, Z3, Z4, Z5 oraz napięcia źródłowe o wartościach skutecznych zespolonych: E1, E3, E4, E6. Celem rozważań jest obliczenie prądów gałęziowych: I1, I2, I3, I4, I5, I6. Dla rozpatrywanego obwodu na podstawie pierwszego prawa Kirchhoffa możemy napisać trzy równania liniowo niezależne, wilżące prądy gałęziowe dla węzła 1 I1 + I2 - I3 = 0 dla węzła 2 I3 + I5 + I6 = 0 (1) dla węzła 3 I4 - I6 - I1 = 0 Wypisując równania na podstawie drugiego prawa Kirchhoffa wybieramy oczka liniowo niezależne. Przyjmujemy zwroty obiegowe oczek zaznaczone na rys. i na podstawie drugiego prawa Kirchhoffa piszemy następujące trzy równania liniowo niezależne: (2) Korzystając z równań (1) możemy prądy I2, I4, oraz I5, wyrazić w zależności od prądów I1, I3, I6 a mianowicie (3) Podstawiamy równania (3) do równań (2) i otrzymujemy (4) Porządkujemy równania (4) względem prądów gałęziowych (5) W budowie równań (5) występuje prawidłowość pozwalająca zapisać je w postaci (6) przy czym przyjęto następujące oznaczenia: (7) Wyjaśnimy sens fizyczny i podamy definicje wielkości w równaniach (7). Prądu I1, I2, uraz I3 (ze wskaźnikiem prim) nazywamy prądami oczkowymi odpowiednio oczka pierwszego, drugiego i trzeciego. Prądem oczkowym (lub cyklicznym) nazywamy prąd umyślony płynący przez wszystkie gałęzie oczka. W gałęzi należącej tylko do jednego oczka (na rys w gałęzi 1, 3 i 6) prąd oczkowy jest równy prądowi gałęziowemu. W gałęzi wspólnej dwóch oczek prąd gałęziowy jest równy sumie lub różnicy geometrycznej prądów oczkowych, zależnie od ich zwrotu. Impedancje o dwóch jednakowych wskaźnikach, a więc impedancje typu Zkk (w rozpatrywanym obwodzie Z11, Z22, Z33) nazywamy impedancjami własnymi oczka. Impedancja własna oczka k-tego jest równa sumie impedancji zespolonych wszystkich gałęzi należących do tego oczka. Impedancja własna oczek przyjmujemy zawsze ze znakiem plus.
(…)
… obwodu elektrycznego mającego trzy oczka liniowo niezależne. Rozważania można uogólnić na przypadek n oczek liniowo niezależnych. Wtedy otrzymamy (9) Układ równań (9) można rozwiązać jedną z metod rozwiązywania niejednorodnego układu równań liniowych, a mianowicie metodą rugowania zmiennych, metodą wyznaczników i metodą macierzową. Omówimy najczęściej stosowane metody - wyznaczników i macierzową…
… (13) a ponieważ iloczyn macierzy odwrotnej przez macierz daną jest równy macierzy jednostkowej, zatem ostatecznie (14) Znając wartości napięć: U'1, U'2,...,U'm, wyznaczamy prądy gałęziowe z zależności napisanych na podstawie prawa Ohma dla poszczególnych gałęzi rozpatrywanego obwodu. Na przykład dla obwodu o schemacie elektrycznym przedstawionym na rys. znając wartości napięć U'1, U'2, i U'3…
… z zależności napisanych na podstawie prawa Ohma dla poszczególnych gałęzi rozpatrywanego obwody. Obwód przedstawiony na rysunku zawiera dwa źródła sterowane: źródło prądu sterowane prądem Iź=kI oraz źródło napięcia sterowane prądem E=ၡIź. Metodą potencjałów węzłowych obliczamy prądy w gałęziach oraz prądy źródłowe Iź i napięcie źródłowe E. Dane: Z1=2ၗ; Z2=1ၗ; Z3=j1ၗ; Z4=-j1ၗ; E4=6V; ၡ=1V/A; k=4A…
… wyznaczenia macierzy I' z równania (14) mnożymy lewostronnie to równanie przez macierz odwrotną względem macierzy impedancji włW celu wyznaczenia macierzy I (15) Ponieważ iloczyn macierzy odwrotnej przez macierz daną jest równy macierzy jednostkowej, ostatecznie więc otrzymamy (16) Obliczanie macierzy odwrotnej Z-1 jest najbardziej pracochłonnym fragmentem obliczeń; musi być przy tym spełniony…
… się na definicjach impedancji własnych oczek Zkk, impedancji wzajemnych oczek Zkl, oraz napięć źródłowych oczkowych Ekk w sposób mnemotechniczny bezpośrednio na podstawie danego schematu elektrycznego rozpatrywanego obwodu, wpisujemy elementy macierzy impedancji Z i macierzy napięć źródłowych oczkowych E. (3) Obliczamy macierz odwrotną Z-1 względem macierzy impedancji Z. (4) Obliczamy macierz kolumnową prądów…
... zobacz całą notatkę





Komentarze użytkowników (0)