To tylko jedna z 20 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
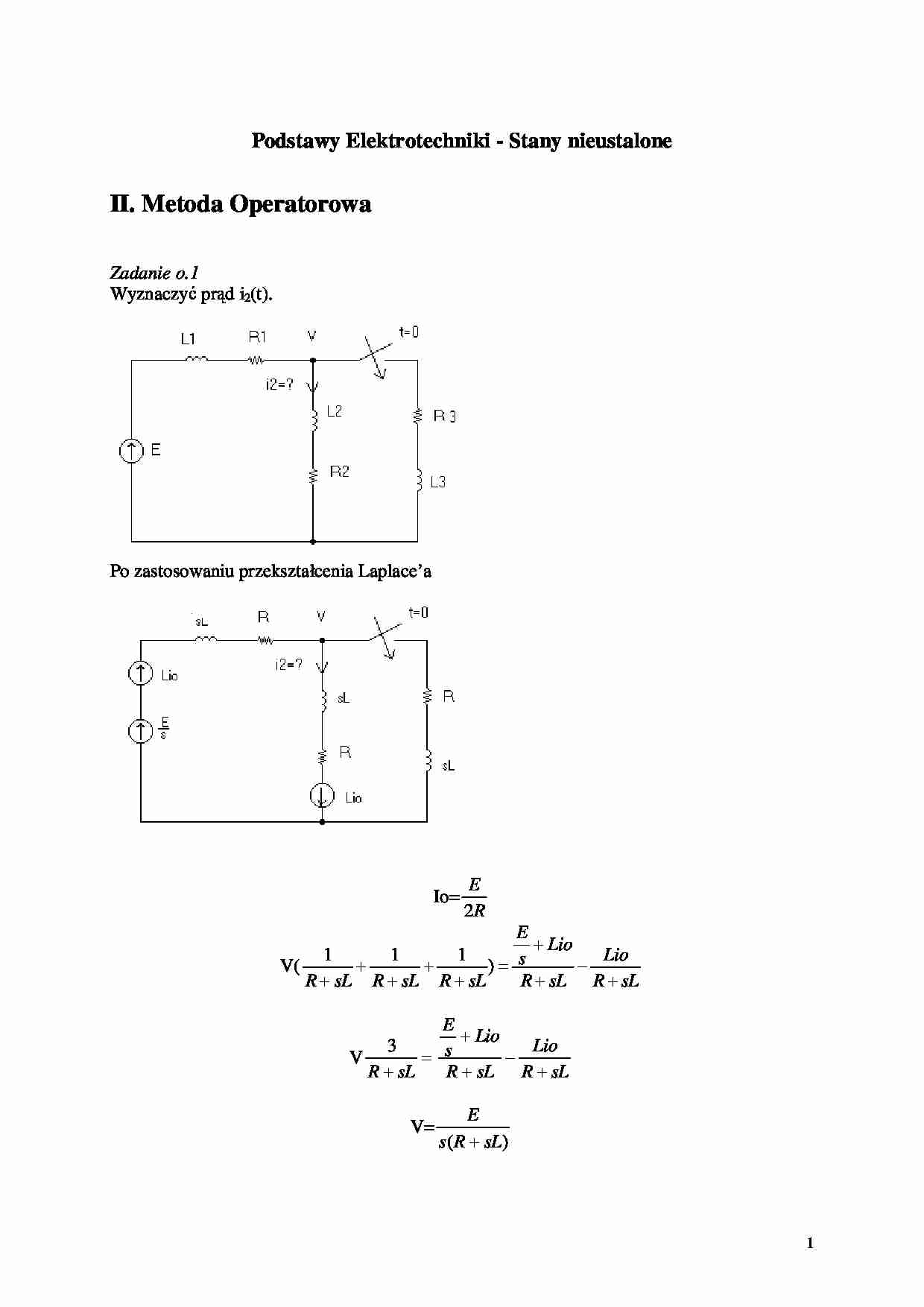


1 Podstawy Elektrotechniki - Stany nieustalone II. Metoda Operatorowa Zadanie o.1 Wyznaczyć prąd i2(t). Po zastosowaniu przekształcenia Laplace’a Io= R E 2 V( sL R Lio sL R Lio s E sL R sL R sL R + − + + = + + + + + ) 1 1 1 V = + sL R 3 sL R Lio sL R Lio s E + − + + V= ) ( sL R s E + 2 2 I (s)= ) ( 3 ) ( 3 s L R Ls E sL R s E sL R V + = + = + ] 3 3 [ 3 3 ) ( 2 t L R t L R e R E R E e R E R E t i − − − = − + = Zadanie o.2 Obliczyć napięcie na zaciskach wyłącznika w chwili t=0 i napięcia na C1 i C2 w chwili t=T. a) t=0: ) 2 1 ( 1 2 2 ) 2 1 ( 1 2 1 2 1 2 ) ( 3 3 3 3 3 3 3 3 3 RC s R E RC RC s EC s RC EC s C s RC s E s C R s E s J + = + = + = + = + = t RC e R E s J L t i 3 2 1 1 2 )} ( { ) ( − − = = 3 3 3 3 2 1 3 2 1 3 3 0 2 1 3 3 0 2 1 3 0 3 3 1 ( ] 2 2 [ 2 ] 2 [ 2 1 2 1 ) ( 1 ) ( RC t RC t t RC t t RC t c e E RC e RC R C E e RC R E C dt e R E C dt t i C t U − − − − − = + − = = − = = = ∫ ∫ t RC t RC R e E R E R t i t U 3 3 2 1 2 1 2 Re 2 ) ( ) ( − − = = = ) 2 1 1 ( 2 ) 1 ( ) ( ) ( ) ( 3 3 3 3 2 1 2 1 2 1 2 1 3 t RC t RC t RC RC R c wyl e e E e E e E t U t U t U − − − − + − = + − = + = b) t=T ) ( 1 1 ) ( ) ( 1 ( ) ( 1 ) ( ) ( ) ( 1 ) ( 2 1 2 1 2 1 2 1 2 1 2 1 2 1 C C RC s R E C C R C C RC s C C E C C Rs C C E C C s R s E s J + + = + + + + = + + + = + + = t C C R e R E s J L t J ) ( 1 1 2 1 )} ( { ) ( + − − = = Obliczamy napięcie na C1 i C2 pamiętając e: Cz=C1+C2 3 ) 1 ( ) ( ) ( ) ( ) ( ] ) ( [ 1 ) ( 1 ) ( ) ( ) ( 1 2 1 2 1 ) ( 1 2 1 2 1 0 ) ( 1 2 1 0 ) ( 1 0 2 1 2 1 2 1 2 1 2 1 t C C R t C C
(…)
… ) )
Zadanie o.12
Wyznaczyć UL(t) dla napięcia zasilania e(t) jak na wykresie.
17
Napięcie wymuszające:
e(t ) = E m sin ωt1(t ) + E m sin ωt1(t −
T
)
2
T
E ( s) = E m
− s
1
1
+ Em e 2
s − jω
s − jω
Odpowiedź układu:
T
−s
E (s)
1 + e 2
U L (s) =
sL = E m
R + sL
s
=
s
( s − jω )(s + R )
L
A
B
+
s−a s+b
R
)
L
A( s + b) + B(s − a )
s
=
(s − a )(s + b)
( s − a)(s + b)
As + Bs + Ab − Ba = s
( s − jω…
... zobacz całą notatkę






Komentarze użytkowników (0)