

Fragment notatki:
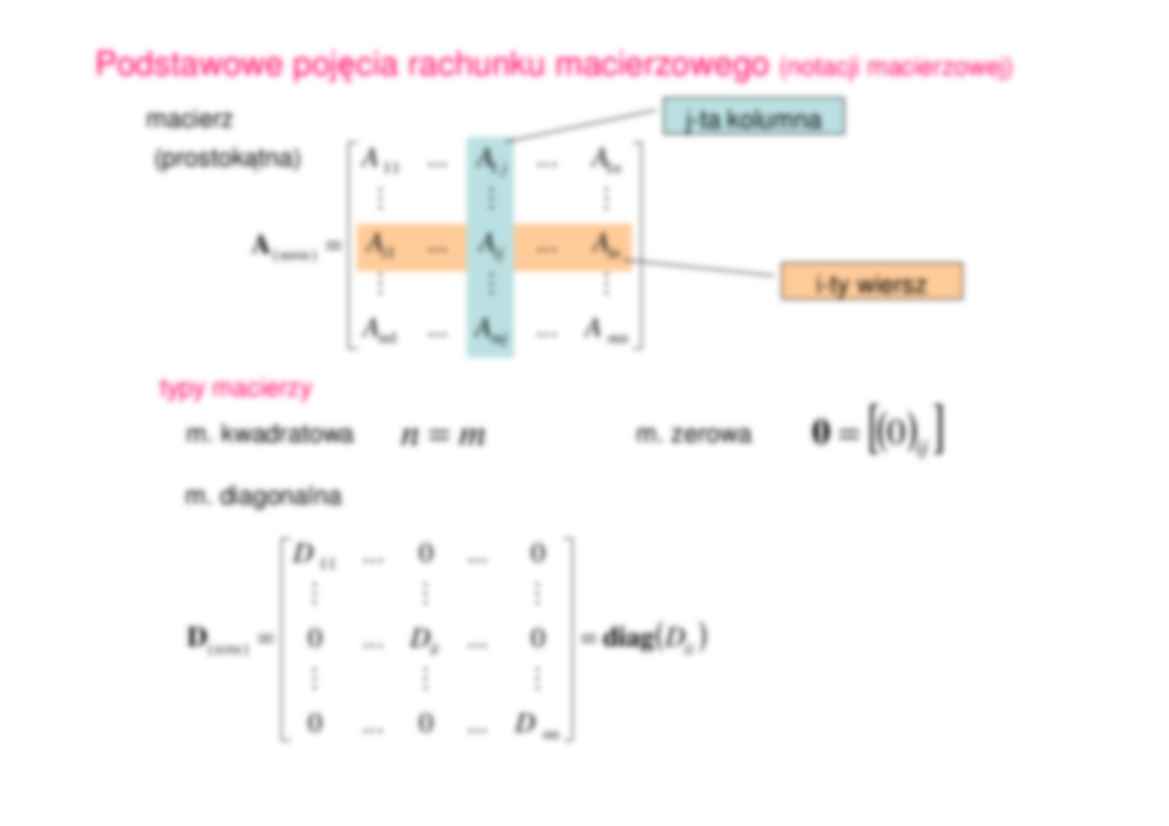
Plan wykładu 1. Przypomnienie – rachunek macierzowy 2. Modelowanie komputerowe-podstawowe pojęcia 3. Problem brzegowy statyki 4. Wprowadzenie do MES na przykładzie problemu statyki 5. Przykłady zastosowań MES - Metoda Elementów Skończonych FEM - Finite Element Method Cel wykładu 1. Podstawowa wiedza z zakresu modelowania komputerowego 2. Usystematyzowanie wiedzy inŜynierskiej zezwalające na świadome uŜywanie oprogramowania inŜynierskiego (Robot, Z_Soil i inne) Rachunek macierzowy (przypomnienie) Podstawowe pojęcia rachunku macierzowego Działania i relacje na macierzach mnoŜenie macierzy operacje na wektorach w notacji macierzowej Układ równań liniowych typy macierzy macierz = × mn mj m in ij i n j n m A A A A A A A A A ... ... ... ... ... ... 1 1 1 1 11 ) ( M M M M M M A typy macierzy m. kwadratowa m n = m. diagonalna ( ) ii nn ii n n D D D D diag D = = × ... 0 ... 0 0 ... ... 0 0 ... 0 ... 11 ) ( M M M M M M m. zerowa ( ) [ ] ij 0 = 0 (prostokątna) Podstawowe pojęcia rachunku macierzowego (notacji macierzowej) j-ta kolumna i-ty wiersz ( ) [ ] = ≠ = = = = × j i j i ij n n 1 0 1 1 ... 0 ... 0 0 ... 1 ... 0 0 ... 0 ... 1 ) ( δ diag I M O M M M M O M m. jednostkowa m. symetryczna - kwadratowa, taka, Ŝe: , ji ij A A = transpozycja macierzy = ⇒ = × × mn n m T m n mn m n n m A A A A A A A A L M M M M L M M 1 1 11 ) ( 1 1 11 ) ( ... ... ... ... A A ( ) T T A A = T A A = uwaga: czasem oznaczana teŜ: ' A A ≡ T macierz kolumnowa (wektor) = × m m a a M 1 ) 1 ( a macierz wierszowa [ ] n n b b L , 1 ) 1 ( = × b Działania i relacje na macierzach dodawanie n j m i C B A ij ij ij , , 1 , , , 1 , K K = = + = ⇔ + = C B A n j m i B A ij ij , , 1 , , , 1 , , K K = = = ⇔ =
(…)
… ∂w
+
γ yz =
B
∂z ∂y
B - macierz operatorów róŜniczkowania
u
v
w
równania równowagi (3D)
σ ij ,i +b j = 0 ⇔
∂σ xx ∂σ xy ∂σ xz
+
+
+ bX = 0
∂x
∂y
∂z
∂σ xy ∂σ yy ∂σ yz
+
+
+ bY = 0 ⇔
∂x
∂y
∂z
∂σ xz ∂σ yz ∂σ zz
+
+
+ bZ = 0
∂x
∂y
∂z
•
BT ⋅ σ + b = 0 ⇔
∂ X 0 ∂ Y 0 ∂ Z 0
0 ∂ ∂
0
0 ∂Z
Y
X
0
∂ Z ∂ X ∂Y
440 40 244444
1
4 4
3
BT
B - macierz operatorów…
… )ε yy + vε xx
4
3
(1 +ν )(1 − 2ν ) 144444 2444444
=
równania równowagi:
ε
xx
∂σ xx ∂σ xy
+
+ bX = 0
∂x
∂y
T
⇔ B ⋅σ + b = 0
∂σ xy ∂σ yy
+
+ bY = 0
∂x
∂y
+ε
yy
zz
Płaski stan napręŜenia (PSN) plane stress
geometryczne: wymiary w dwóch kierunkach znacznie większe niŜ trzecim (grubość),
obciąŜenia (czynne i reakcje więzów): tworzą układ płaski w pł. XY
więzy…
… 1 x
L
L
L
ξ=
1
N1 = 1 − ξ
u2
=
+
1
N2 = ξ
x
L
N 2 ⋅ u2
Interpolacja w 2D. Zasady zgodności
2
1.
N1 ( x1 ) = 1,
1, a = b
⇒ N a ( xb ) = δ ab =
N 2 ( x1 ) = N 3 ( x1 ) = N 4 ( x1 ) = 0
0, a ≠ b
1
3
4
interpolacja funkcji stałej powinna dać w
wyniku stałą
c
2
c
3
c
c
c
1
c = u1 = u 2 = u 3 = u 4 ⇒ u ( x ) = c
Nen
∑ cN (x ) = c ⇒
a =1
a
2.
Nen
∑ N (x ) = 1
a =1
a
4
1,2 zasady…
… w
ε xx
∂u ∂v ∂ X 0 0
γ xy = + ε 0 ∂
∂y ∂x 0
⇔ ε = B⋅u ⇔
yy Y
γ xy
∂w ∂Y ∂ X 0
ε zz = =
∂z ε zz 0 0 ∂Z
∂u ∂w γ xz ∂ Z 0 ∂ X
γ xz = +
∂z ∂x
γ yz
0 ∂ Z ∂Y
44 44
1 2 3
∂v ∂w
γ yz = + B
∂z ∂y B - macierz operatorów róŜniczkowania
równania równowagi (3D)
σ ij ,i +b j = 0 ⇔
∂σ xx ∂σ xy ∂σ xz
+ + + bX = 0
∂x ∂y…
… − 2ν ) 0 0 b 0 γ xy 1 −ν 2(1 −ν )
σ zz a a 0 1 ε zz (= 0 )
14444 244444 4 3
D
σ zz =
Ev
(1 +ν )(1 − 2ν )
(ε xx + ε yy ) = ν (σ xx + σ yy )
dla v ≠ 0, σ ≠ 0
zz
σ xx + σ yy =
E
[
(1 +ν )(1 − 2ν ) 144444 2444444 4 3
]
(1 −ν )ε xx + vε yy + (1 −ν )ε yy + vε xx
=
równania równowagi:
ε +ε
xx yy
∂σ xx ∂σ xy
+ + bX = 0
∂x ∂y
⇔ B ⋅σ + b = 0
T
∂σ xy ∂σ yy…
…. transponowanych w
odwrotnej kolejności
T
= B ⋅A
T
T
I ⋅ A = A⋅I = A
0⋅ A = A⋅0 = 0
macierz jednostkowa jest
elementem neutralnym mnoŜenia
operacje na wektorach w notacji macierzowej
a1
T
a = M = [a1 , K an ] ,
an
iloczyn skalarny :
b1
T
b = M = [b1 , K bn ]
bn
n
c = a o b ⇔ aT b = ∑ ai bi
i =1
notacja wskaźnikowa z umową sumacyjną Einsteina
iloczyn diadyczny:
a1b1
C…
… im odkształceń δε ij , zachodzi równość pracy wirtualnej sił
wewnętrznych i zewnętrznych.
∂Ω t
T.S. w notacji macierzowej (3d)
b
Szukamy pól:
Ω
t
u = [u, v, w]
T
∂Ωu
wektor przemieszczeń
[
ε = ε xx , ε yy , γ xy , ε zz , γ xz , γ yz
[
]
T
σ = σ xx ,σ yy ,σ xy ,σ zz ,σ xz ,σ yz
wektor odkształceń
]
T
(γ
ij
= 2ε ij )
wektor napręŜeń
Dane:
b = [bX , bY , bZ ]
T
t = [t X , tY , t Z ]
wektor sił masowych (grawitacja…
…
właściwości mnoŜenia macierzy:
A⋅B ≠ B⋅A mnoŜenie m. jest (na ogół) nieprzemienne,
(nawet dla m. kwadratowych)
A ⋅ (B + C) = A ⋅ B + A ⋅ C rozdzielność względem dodawania
A ⋅ (B ⋅ C ) = (A ⋅ B ) ⋅ C łączność
(A ⋅ B )
transpozycja iloczynu m.=
= B ⋅A
T T T
iloczynowi m. transponowanych w
odwrotnej kolejności
I ⋅ A = A⋅I = A macierz jednostkowa jest
elementem neutralnym mnoŜenia
0⋅ A = A⋅0 = 0
operacje…
… róŜniczkowania
σ xx
σ
yy
σ xy
σ zz
σ xz
σ yz
+
bX
b = 0
Y
bZ
równania fizyczne – związki konstytutywne (3D)
σ ij = Dijkl ε kl
postać ogólna dla materiału anizotropowego, 36 stałych
Dijkl tensor konstytutywny 4-go rzędu
Dla materiału Hooke’a, izotropowego tylko 2 stałe są niezaleŜne. Istnieją róŜne
moŜliwości ich wyboru:
i odpowiadające im róŜne formy prawa…
... zobacz całą notatkę

Komentarze użytkowników (0)