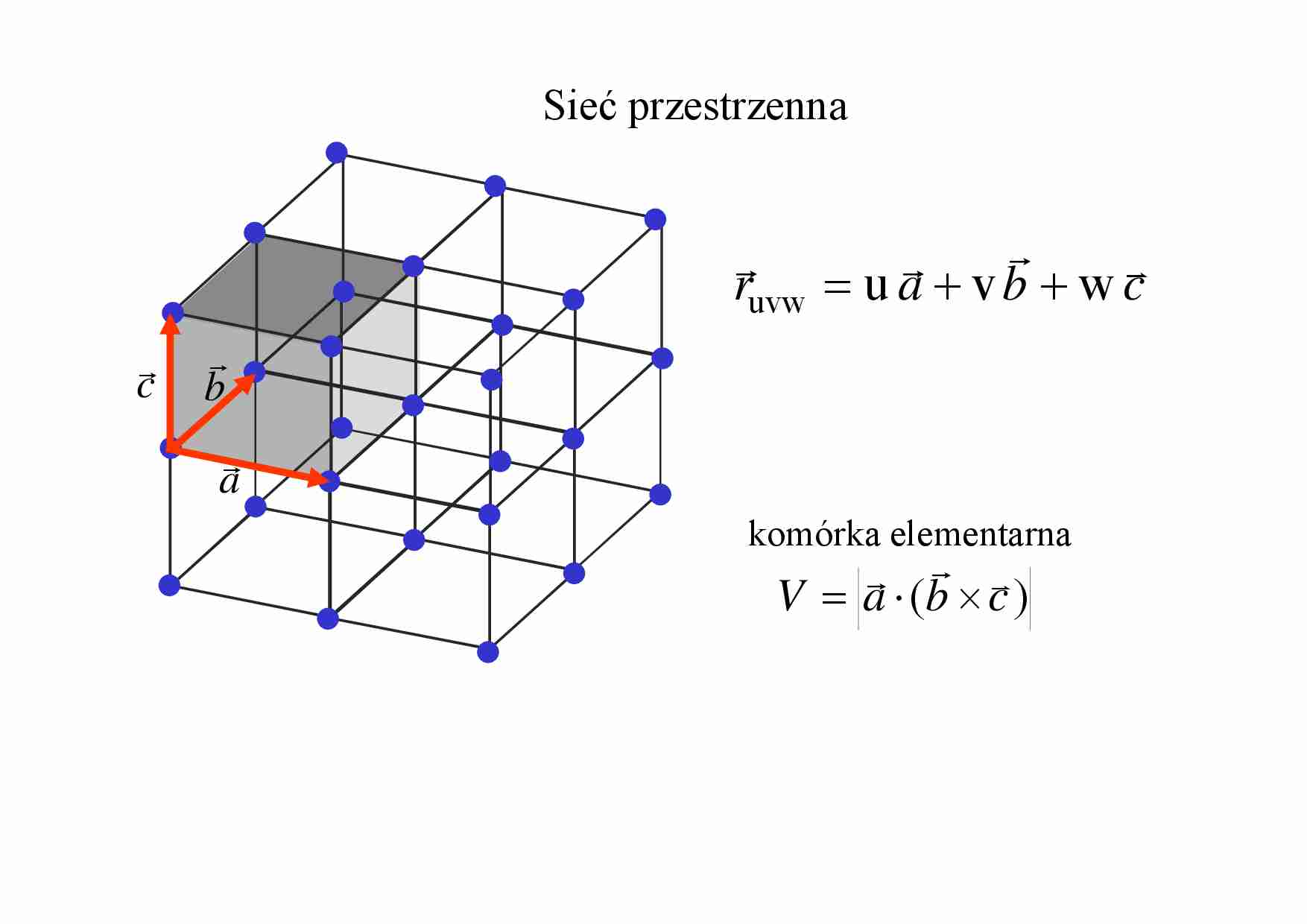
Sieć przestrzenna
r
r
r
v
ruvw = u a + v b + w c
r
c
r
b
r
a
komórka elementarna
r r v
V = a ⋅ (b × c )
Układy krystalograficzne (7)
i
Sieci Bravais (14)
Triclinic (P)
a ≠ b ≠ c, α ≠ β ≠ γ ≠ 90ο
Monoclinic (P)
a ≠ b ≠ c, α = γ = 90ο, β ≠ 90ο
Monoclinic (C)
a ≠ b ≠ c, α = γ = 90ο, β ≠ 90ο
Orthorhombic (P)
a ≠ b ≠ c, α = β = γ = 90ο
Orthorhombic (C)
a ≠ b ≠ c, α = β = γ = 90ο
Orthorhombic (F)
Orthorhombic (I)
a ≠ b ≠ c, α = β = γ = 90ο a ≠ b ≠ c, α = β = γ = 90ο
Hexagonal (P) HCP
a= b ≠ c, α = β = 90o, γ = 120o
Tetragonal (P)
a= b ≠ c, α = β = γ =90o
Rhombohedral (R)
a = b = c, α = γ = β ≠ 90ο
Tetragonal (I)
Cubic (P)
a= b = c, α = β = γ = 90o
Cubic (I) BCC
a= b = c, α = β = γ = 90o
Cubic (F) FCC
a= b = c, α = β = γ = 90o
Grupy punktowe (32)
zbiór przekształceń symetrii, w których węzeł pozostaje nieruchomy a sieć
przechodzi sama w siebie
obroty, odbicie zwierciadlane, inwersja
Grupy przestrzenne (230)
sieci Bravais + grupy punktowe
Proste sieciowe [u,v,w]
[1,1
,2]
kierunki symetrycznie równoważne
np. w układzie regularnym:
= [100], [-1 0 0], [010]......
z
Płaszczyzny sieciowe - wskaźniki Millera
2
też (323)
r
c r
b
r
a
x
3
y
2
•znaleźć współrzędne przecięcia płaszczyzny z osiami : 2, 3, 2
•utworzyć odwrotności tych liczb: 1/2, 1/3, 1/2
•znaleźć trzy najmniejsze liczby całkowite o tym samym stosunku: 3, 2, 3
•liczby te zapisane w nawiasie są wskaźnikami płaszczyzny (hkl) - (323)
Płaszczyzny sieciowe - wskaźniki Millera
Przykłady u układzie regularnym
• Punkt przecięcia: a, 0, 0
• Wskaźniki Millera: (111)
(222)
• Punkt przecięcia: a, a, ∞
• Wskaźnik Millera: (110)
• Punkt przecięcia: a, ∞, ∞
• Wskaźnik Millera: (100)
• Punkt przecięcia: (1/2)a, a, ∞
•w jednostkach a: 1/2, 1, ∞
• Wskaźnik Millera: (210)
trzy zaznaczone płaszczyzny są dzięki symetrii równoważne,
w układzie regularnym jest ich 6:
(100), (010), (001), (100), (010), (001),
zbiór równoważnych płaszczyzn oznaczamy:
{hkl}, np. {100}
W układach regularnych kierunek [hkl] jest prostopadły do płaszczyzny (hkl)
Sieć płaska - dwuwymiarowa
r
r
r
ruv = u a + v b
r
b
r
a
Sieć ukośna
komórka elementarna
r r v
V = a ⋅ (b × c )
r r
S = a ×b
r r r
S = n ⋅ (a × b )
Dwuwymiarowe sieci Bravais (5)
r
b γ
r
b
r
a
ukośna
r
b
r
a
r
a
prostokątna
r
b
r
a'
prostokątna
centrowana
r
b
r
b
r
a
kwadratowa, a=b
60o
r
a
heksagonalna a=b
Dwuwymiarowe grupy punktowe (10)
ukośna
1
2
m
2mm
prostokątna
(centrowana)
2mm
kwadratowa
4
4mm
3
6
heksagonalna
3mm
6mm
3
6
Sieci dwuwymiarowe, dwuwymiarowe grupy punktowe (10), grupy przestrzenne (17)
Grupa
Uk ład i symbol sieci punktowa
skośny(p)
1
2
prostokątny (p)
m
prostokątny
centrowany
(c)
2mm
kwadratowy (p)
heksagonalny (p)
4
4mm
3
3m
6
6m
Symbole grup
przestrzennych
pełne
skrócone
p1
p211
p1m1
p1g1
c1m1
p2mm
p2mg
p2gg
c2mm
p4
p4mm
p4gm
p3
p3m1
p31m
p6
p6mm
p1
p2
pm
pg
cm
pmm
pmg
pgg
cmm
p4
p4m
p4g
p3
p3m1
p31m
p6
p6m
Nr grupy
przestrzennej
1
2
3
4
5
6
7
8
... zobacz całą notatkę





Komentarze użytkowników (0)