To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Koncentracja nośników w półprzewodnikach
Prawdopodobieństwem zajmowania danego stanu energetycznego przez fermiony rządzi
statystyka Fermiego-Diraca:
1
f (E) =
e
E − EF
kT
+1
, gdzie k jest stałą Boltzmanna, zaś E F to energia Fermiego
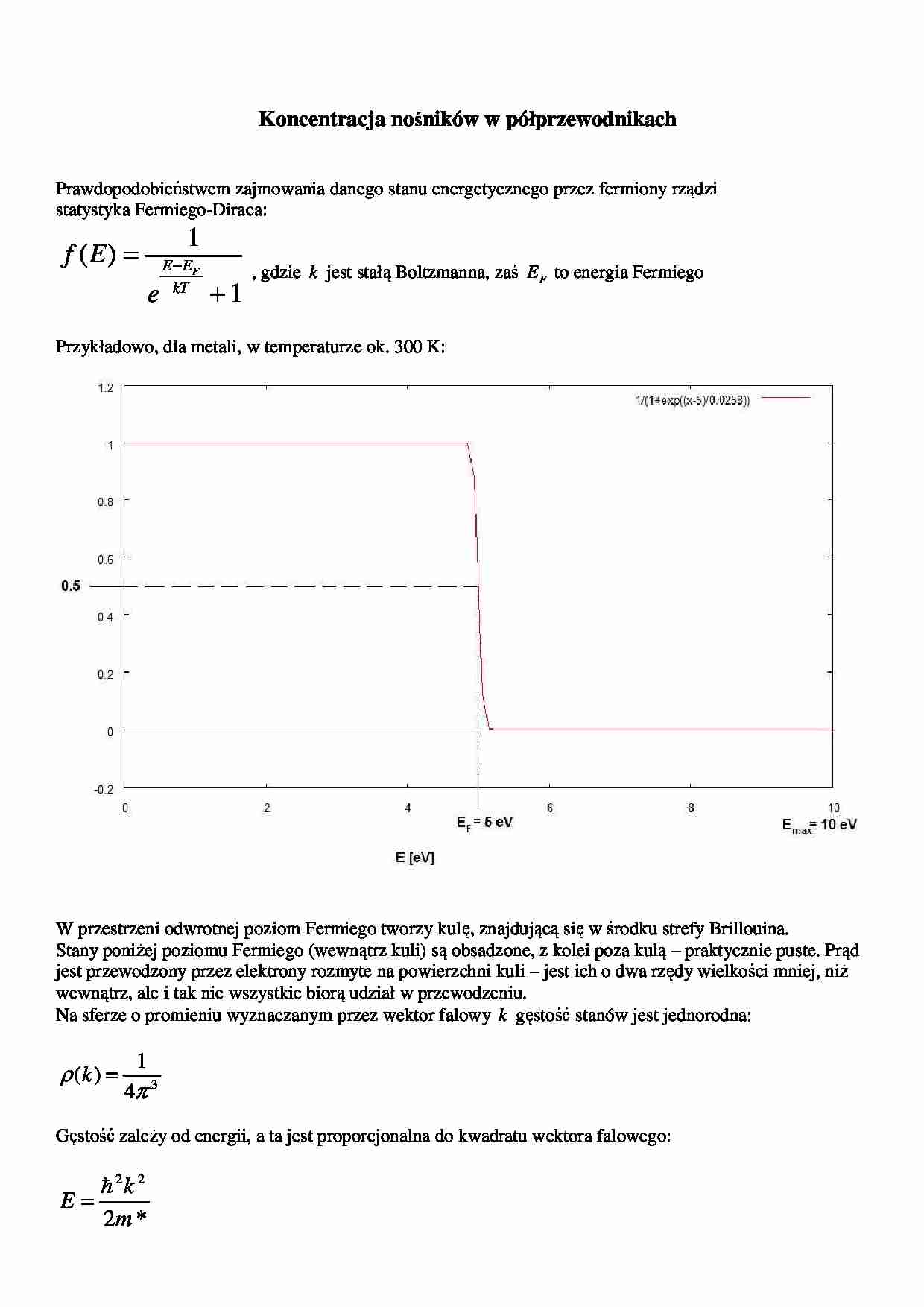
Przykładowo, dla metali, w temperaturze ok. 300 K:
W przestrzeni odwrotnej poziom Fermiego tworzy kulę, znajdującą się w środku strefy Brillouina.
Stany poniżej poziomu Fermiego (wewnątrz kuli) są obsadzone, z kolei poza kulą – praktycznie puste. Prąd
jest przewodzony przez elektrony rozmyte na powierzchni kuli – jest ich o dwa rzędy wielkości mniej, niż
wewnątrz, ale i tak nie wszystkie biorą udział w przewodzeniu.
Na sferze o promieniu wyznaczanym przez wektor falowy k gęstość stanów jest jednorodna:
ρ (k ) =
1
4π 3
Gęstość zależy od energii, a ta jest proporcjonalna do kwadratu wektora falowego:
h2k 2
E=
2m *
Gęstość nośników możemy wyrazić jako stosunek ich koncentracji do objętości: ρ (k ) =
stąd: dN =
ρ ( k ) dV =
1
4π 3
4πk dk =
2
k2
dN
dV
dk
π2
Jednocześnie możemy napisać: dN = ρ ( E ) dE
k 2 dk
Łącząc powyższe równości uzyskujemy: ρ ( E ) = 2
π dE
h2k 2
dE h 2 k
=
Korzystając z zależności E =
obliczamy pochodną:
2m *
dk m *
k2 m*
k m*
ρ (E) = 2 2 = 2 2
π h k π h
Z równania E =
h2k 2
2m * E
mamy również wyrażenie na k : k =
, które wstawiamy tego powyżej:
2m *
h
21 2 (m*) 3 2
ρ (E) =
π 2h 3
E
- jest to zależność prawdziwa na dnie pasma przewodnictwa, tam, gdzie nośniki przewodzą prąd
Nośnikami ładunku mogą być zrówno elektrony, o rozkładzie:
1
f ( Ee ) =
e
Ee − EF
kT
+1
,
jak i dziury, oznaczające brak elektronu:
f ( E d ) = 1 − f ( E e ) → E d = − E e , stąd:
1
f ( Ed ) =
Ed + EF
kT
e
+1
- poziom Fermiego jest taki sam dla elektronów i dziur, znajduje się mniej więcej w połowie przerwy
Eg
energetycznej, tam też wybieramy poziom zerowy: przeskalowujemy energię E e →
+ Ee
2
Koncentracja elektronów w paśmie przewodnictwa – całka po strefie Brillouina:
n=
∞
∫ f ( E ) ρ ( E )dE = ∫ f ( E ) ρ ( E )dE
e
SB
0
=
21 2 (m*)3 2 1 2
Ee dEe
π 2h3
1
Eg
Ee
kT
e e
2 kT
e
−
EF
kT
+1
1
Stosujemy przybliżenie:
Ee
kT
Eg
e e 2 kT e
∞
e
0
∞
=∫
e
n = ∫e
−
Ee
kT
e
−
Eg
2 kT
e
EF
kT
−
EF
kT
1
≈
Ee
kT
+1
Eg
e e 2 kT e
−
EF
kT
=
e
−
Ee
kT
e
−
Eg
2 kT
21 2 (m*)3 2 1 2
⋅
Ee dEe
π 2h 3
0
= const
n=e
−
Eg
2 kT
e
EF
kT
Ee
kT
x=
Zamiana zmiennych:
,
1
E e 2 = (kT )1 2 x 1 2 , dEe = kT dx
∞
21 2 (m*)3 2 (kT )3 2
⋅
⋅ ∫ e − x x1 2 dx
2 3
π h
0
||
π
2
Ostatecznie:
3
2
E
g
m kT − 2 kT EF
n = 2
e kT
2π h 2 e
*
e
- koncentracja elektronów w paśmie przewodnictwa
Wykonując analogiczne obliczenia w przypadku dziur otrzymalibyśmy:
3
2
E
g
m kT − 2 kT − EF
p = 2
e kT
2π h 2 e
*
d
- koncentracja dziur w paśmie walencyjnym
e
EF
kT
Półprzewodniki samoistne
Poziom Fermiego dla półprzewodnika niedomieszkowanego (samoistnego) oznaczamy symbolem
W półprzewodniku takim liczba elektronów jest równa liczbie dziur:
n
... zobacz całą notatkę






Komentarze użytkowników (0)