To tylko jedna z 29 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Wektory
Kinematyka
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Wektory
Wielkości fizyczne to skalary lub wektory.
Skalar – wielkość określona przez wartość.
Przykłady: ciśnienie, długość, gęstość.
Wektor– wielkość określona przez wartość, kierunek i zwrot.
Przykłady: siła, prędkość, przyspieszenie.
Wektory przedstawiamy graficznie jako strzałki, której długość odpowiada
wartości wektora.
W prostokątnym układzie współrzędnych wektor można rozłożyć na
składowe.
Wektor a przedstawiamy w postaci:
a ax ,a y
a
Wektor a
y
ay
ax
x
Wektor a w dwuwymiarowym
prostokątnym układzie współrzędnych
składowa x-owa wektora składowa y-owa wektora
2
2
Długość wektora a : a a x a y
Aby dodać dwa wektory należy dodać odpowiednio współrzędne tych
wektorów:
a a x , a y
b b x , b y
a b a x bx , a y b y
Graficznie dodajemy wektory metodą równoległoboku:
•Przesuwamy wektory tak, aby ich początki były w jednym punkcie,
a
b
a
•Budujemy równoległobok,
b
a b
•Przekątna równoległoboku jest szukaną sumą a b
a
a
b
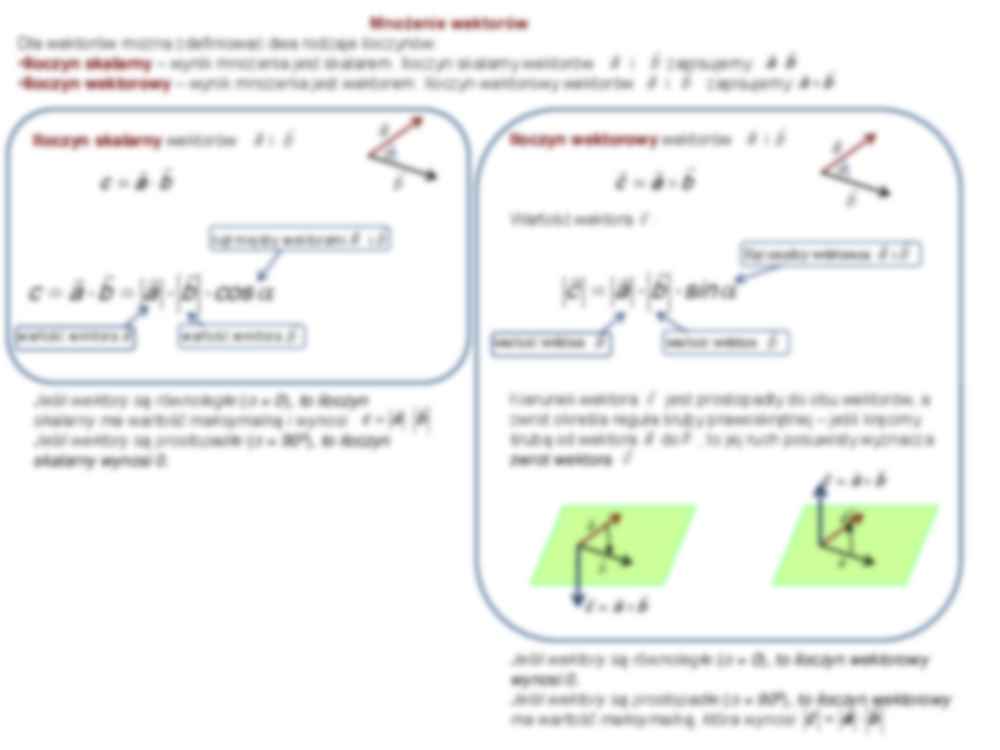
Mnożenie wektorów
Dla wektorów można zdefiniować dwa rodzaje iloczynów:
•Iloczyn skalarny – wynik mnożenia jest skalarem. Iloczyn skalarny wektorów a i b zapisujemy: a b
•Iloczyn wektorowy – wynik mnożenia jest wektorem. Iloczyn wektorowy wektorów a i b zapisujemy: a b
a
Iloczyn skalarny wektorów a i b
α
c a b
Iloczyn wektorowy wektorów a i b
kąt między wektorami a i b
c a b a b cos
wartość wektora
α
c a b
b
wartość wektora a
a
b
Wartość wektora c :
Kąt między wektorami
a ib
c a b sin
b
Jeśli wektory są równoległe (α = 0), to iloczyn
skalarny ma wartość maksymalną i wynosi c a b
Jeśli wektory są prostopadłe (α = 900), to iloczyn
skalarny wynosi 0.
a
wartość wektora
wartość wektora
b
Kierunek wektora c jest prostopadły do obu wektorów, a
zwrot określa reguła śruby prawoskrętnej – jeśli kręcimy
śrubą od wektora a do b , to jej ruch posuwisty wyznacza
zwrot wektora c
c a b
b
a
a
b
c a b
Jeśli wektory są równoległe (α = 0), to iloczyn wektorowy
wynosi 0.
Jeśli wektory są prostopadłe (α = 900), toiloczyn wektorowy
ma wartość maksymalną, która wynosi c a b
Kinematyka – opis ruchu
Ruch to zmiana położenia ciała względem innego ciała lub ogólniej - względem wybranego układu odniesienia.
Punkt materialny – ciało posiadające masę i zaniedbywalnie małe rozmiary (np. ruch Ziemi po orbicie wokółsłonecznej
można rozpatrywać jako ruch punktu materialnego, ale ruch obrotowy Ziemi – już nie).
Tor – zbiór kolejnych położeń poruszającego się punktu.
Droga – długość toru.
Przesunięcie – wektor, którego początek jest w początkowym położeniu, a koniec w końcowym położeniu poruszającego
się punktu. Długość wektora przesunięcia na ogół nie jest
... zobacz całą notatkę






Komentarze użytkowników (0)