To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Geometria wykreślna
Wykład 3
Obraz płaszczyzny
Odwzorowanie płaszczyzny polega na przedstawieniu elementów które do tej płaszczyzny przynależą. Aby w jednoznaczny sposób określić płaszczyznę wystarczy podać obraz:
Trzech punktów należących do płaszczyzny,
Dwóch prostych równoległych lub przecinających się,
Prostej i punktu nie leżącego na tej prostej
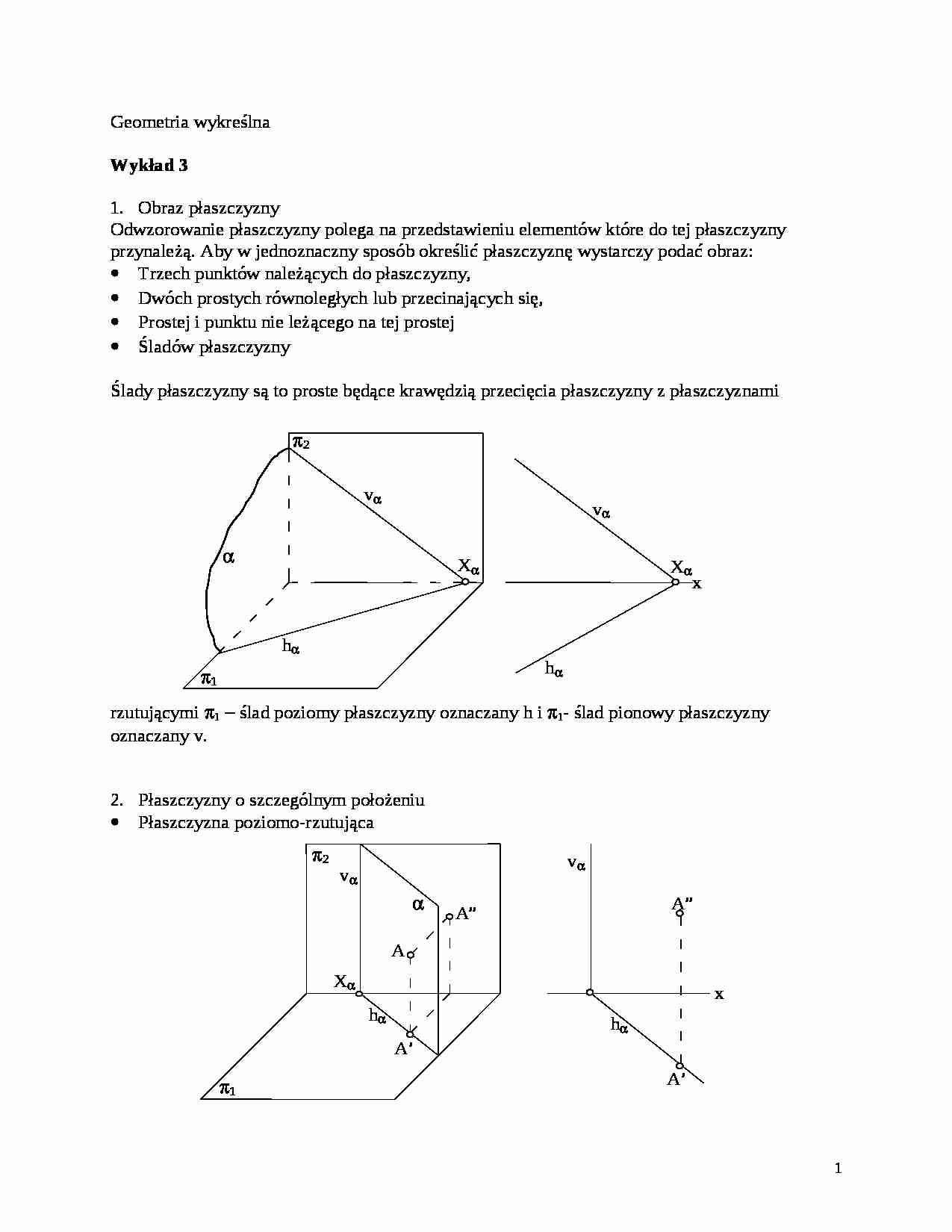
Śladów płaszczyzny
Ślady płaszczyzny są to proste będące krawędzią przecięcia płaszczyzny z płaszczyznami rzutującymi ślad poziomy płaszczyzny oznaczany h i - ślad pionowy płaszczyzny oznaczany v.
Płaszczyzny o szczególnym położeniu
Płaszczyzna poziomo-rzutująca
Płaszczyzna pionowo-rzutująca
Przynależność prostej i płaszczyzny
Prosta leży na płaszczyźnie jeżeli jej dwa punkty leżą na płaszczyźnie. W bardzo łatwy sposób można stwierdzić czy prosta leży na płaszczyźnie wykazując czy ślady prostej leżą na śladach płaszczyzny. Jeżeli prosta leży na płaszczyźnie to jednoimienne ślady prostej leżą na śladach płaszczyzny.
Niezbędna w wielu zadaniach rozwiązywanych na późniejszych etapach poznawania geometrii wykreślnej jest umiejętność wykreślania prostych: poziomej i czołowej leżących na płaszczyźnie dowolnej.
Przynależność punktu i płaszczyzny.
Aby wykazać że punkt należy do płaszczyzny należy znaleźć prostą która leży na płaszczyźnie i na której leży dany punkt Zadania
Narysuj ślady płaszczyzny pionowo-rzutującej nachylonej do rzutni poziomej pod kątem 30 stopni.
Mając dowolną płaszczyznę wykreśl rzuty prostej dowolnej, poziomej i czołowej leżących na tej płaszczyźnie.
Sprawdź czy punkt A dany rzutami leży na płaszczyźnie dowolnej Dana jest płaszczyzna dwoma prostymi równoległymi m i n. Wykreśl rzuty prostej czołowej oddalonej od płaszczyzny o 4cm i leżącej na płaszczyźnie danej tymi dwoma prostymi(ark 1, zad 4).
Dana jest płaszczyzna dwoma prostymi przecinającymi się a i b. Wykreśl rzuty prostej poziomej oddalonej od płaszczyzny o 3cm i leżącej na płaszczyźnie danej tymi dwoma prostymi.
Dane są ślady płaszczyzny dowolnej γ rzut pionowy równoległoboku ABCD. Wykreśl rzut poziomy tego równoległoboku. Dana jest płaszczyzna dwoma prostymi równoległymi m i n oraz rzut poziomy punktu A należącego do tej płaszczyzny. Znajdź rzut pionowy tego punktu.
... zobacz całą notatkę






Komentarze użytkowników (0)