Funkcje falowe w atomie wodoru
Wartości przyjmowane przez liczby kwantowe
n, l, m mają wpływ na postać funkcji falowej
Ψ ( x, y, z ) = Ψ (r , ϑ , ϕ ) = Ψn,l,m (r , ϑ , ϕ )
Ψn,l,m (r , ϑ , ϕ ) = R n,l (r ) ⋅ Yl,m (ϑ , ϕ )
Funkcja, która spełnia równanie Schrödingera, nosi nazwę
ORBITALU
ORBITAL ATOMU WODORU = Funkcja falowa elektronu
w atomie wodoru
Orbitale atomu wodoru (1)
Poboczna liczba kwantowa ma oznaczenia literowe:
l
0
1
2
s
p
d
sharp principal diffuse
3
4
f
fundamental
g
Uwaga! Nie kryje się za tym Ŝaden głęboki sens, to
jest po prostu sposób na łatwiejsze pamiętanie ...
1
Orbitale atomu wodoru (2)
• Orbital 1s: n=1, l=0, m=0
Ψ (x, y, z) = Ψ (r,ϑ,ϕ) = R10(r) ⋅ Y00(ϑ,ϕ)
100
100
R(r ) = 2a0 −3/ 2 ⋅ exp( −
r2R2
1
2
3
Część radialna, R1,0(r)
)
ε oh2
a0 =
= 52,9 pm
πme e 2
1s
0
r
a0
E1 = -13,6 eV
4
5
r/a0
Orbitale atomu wodoru (3)
Y(ϑ , ϕ ) = 1 / 4π
ns
1s
• Część kątowaY00(ϑ,ϕ)
wykres łączy punkty o
jednakowej wartości
funkcji kątowej, czyli
jednakowej gęstości
prawdopodobieństwa
znalezienia elektonu
2
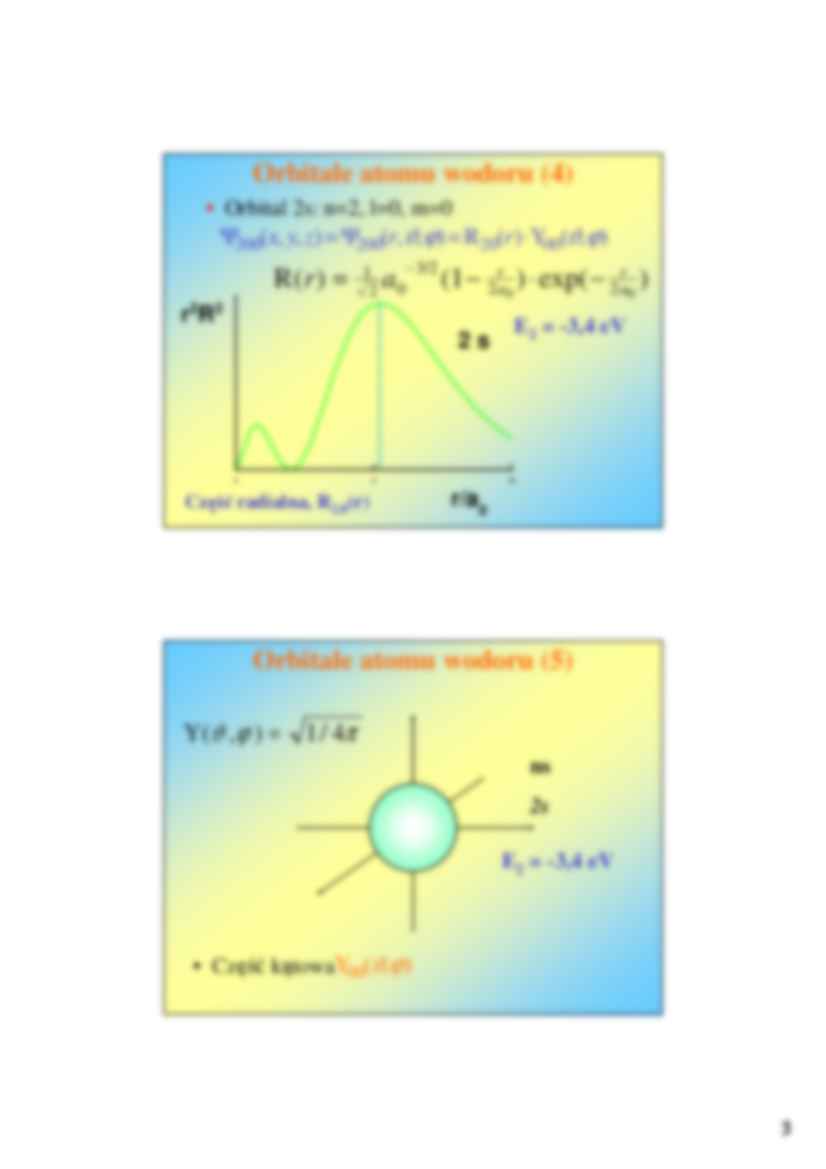
Orbitale atomu wodoru (4)
• Orbital 2s: n=2, l=0, m=0
Ψ200(x, y, z) = Ψ200(r,ϑ,ϕ) = R20(r) ⋅ Y00(ϑ,ϕ)
R(r ) =
1
2
a0 − 3/ 2 (1 − 2 r 0 ) ⋅ exp( − 2 r 0 )
a
a
r2R2
2s
0
5
Część radialna, R2,0(r)
E2 = -3,4 eV
10
r/a0
Orbitale atomu wodoru (5)
Y(ϑ , ϕ ) = 1 / 4π
ns
2s
E2 = -3,4 eV
• Część kątowaY00(ϑ,ϕ)
3
Orbitale atomu wodoru (6)
Orbitale 2p: n=2, l=1, m=0, ±1
Ψ210(x,y,z), Ψ211(x,y,z), Ψ21,-1(x,y,z) ; R21(r)
R 2,1 (r ) =
2
rR
2
1
2
−
a0 5/ 2 ⋅ r ⋅ exp( − 2 r 0 )
a
6
E2 = -3,4 eV
2p
0
5
10
Część radialna, R2,1(r)
15
r/a0
Orbitale atomu wodoru (7)
Y (ϑ,ϕ),Y (ϑ,ϕ),Y 1 (ϑ,ϕ)
10
11
1
E2 = -3,4 eV
Y1,0 (ϑ , ϕ ) = 3 / 4π cosϑ
Y1,1 (ϑ ,ϕ ) = 3 / 4π sin ϑ cosϕ
Y1,-1 (ϑ ,ϕ ) = 3 / 4π sin ϑ sin ϕ
2p z
2p x
2p y
x M = r ⋅ cosϕ ⋅ sin ϑ
y M = r ⋅ sin ϕ ⋅ sin ϑ
z M = r ⋅ cosϑ
4
Orbitale atomu wodoru (8)
orbitale np (2p)
m=0
m=1
z
m= -1
z
z npy
npz
npx
x
y
x
y
płaszczyzna
węzłowa xy
x
y
płaszczyzna
węzłowa yz
płaszczyzna
węzłowa xz
Orbitale atomu wodoru (9)
• Orbital 3s: n=3, l=0, m=0
Ψ300(x, y, z) = Ψ300(r,ϑ,ϕ) = R30(r) ⋅ Y00(ϑ,ϕ)
R 3,0 (r ) =
2
9
−
a0 3 / 2 ⋅ [ 3 −
3
2r
a0
+
2r 2
2
9 a0
r2R2
5
10
15
Część radialna, R3,0(r)
20
r
3a 0
)
E3 = -1,5 eV
3s
0
] ⋅ exp( −
25
Część kątowa
jest taka sama
dla wszystkich
orbitali ns
r/a0
5
Orbitale atomu wodoru (10)
Orbitale 3p: n=3, l=1, m=0, ±1
Ψ310(x,y,z), Ψ311(x,y,z), Ψ31,-1(x,y,z) ; R31(r)
3pz, 3px, 3py
R 3,1 (r ) =
4
27 6
−
r
r
a0 5/ 2 ⋅ (2 − 3a0 ) ⋅ exp( − 3a0 )
E3 = -1,5 eV
r2R2
3p
0
5
10
15
20
25
Część kątowa
jest taka sama
dla wszystkich
orbitali np
r/a0
Część radialna, R3,1(r)
Orbitale atomu wodoru (11)
Orbitale 3d: n=3, l=2, m=0, ±1, ±2
Ψ320(x,y,z), Ψ321(x,y,z), Ψ32,-1(x,y,z), Ψ322(x,y,z),
Ψ32,-2(x,y,z) ; R32(r)
R(r ) =
1
81
−
r
a0 7 / 2 ⋅ r 2 ⋅ exp( − 3a0 )
30
r2R2
E3 = -1,5 eV
3d
0
5
10
Część radialna, R3,2(r)
15
20
25
r/a0
6
Orbitale atomu wodoru (12)
część kątowa
(…)
…
Jeśli elektron w atomie wodoru posiada najniŜszą
moŜliwą energię, to jego stan opisuje orbital 1s
Nawet poziomy 1s, 2s, .. mogą być
rozszczepione !
1s
w polu elektrycznym
i magnetycznym
Elektron zachowuje sie tak, jakby posiadał
"wewnętrzny moment pędu„
Ta własność elektronu nosi nazwę spinu
(Dirac 1928)
Wartość spinu dla elektronu wynosi zawsze 1/2
1
1
1
s
2
2
2
s=
m = − ,+
11
Stan elektronu w atomie wodoru
Ψ…
... zobacz całą notatkę





Komentarze użytkowników (0)