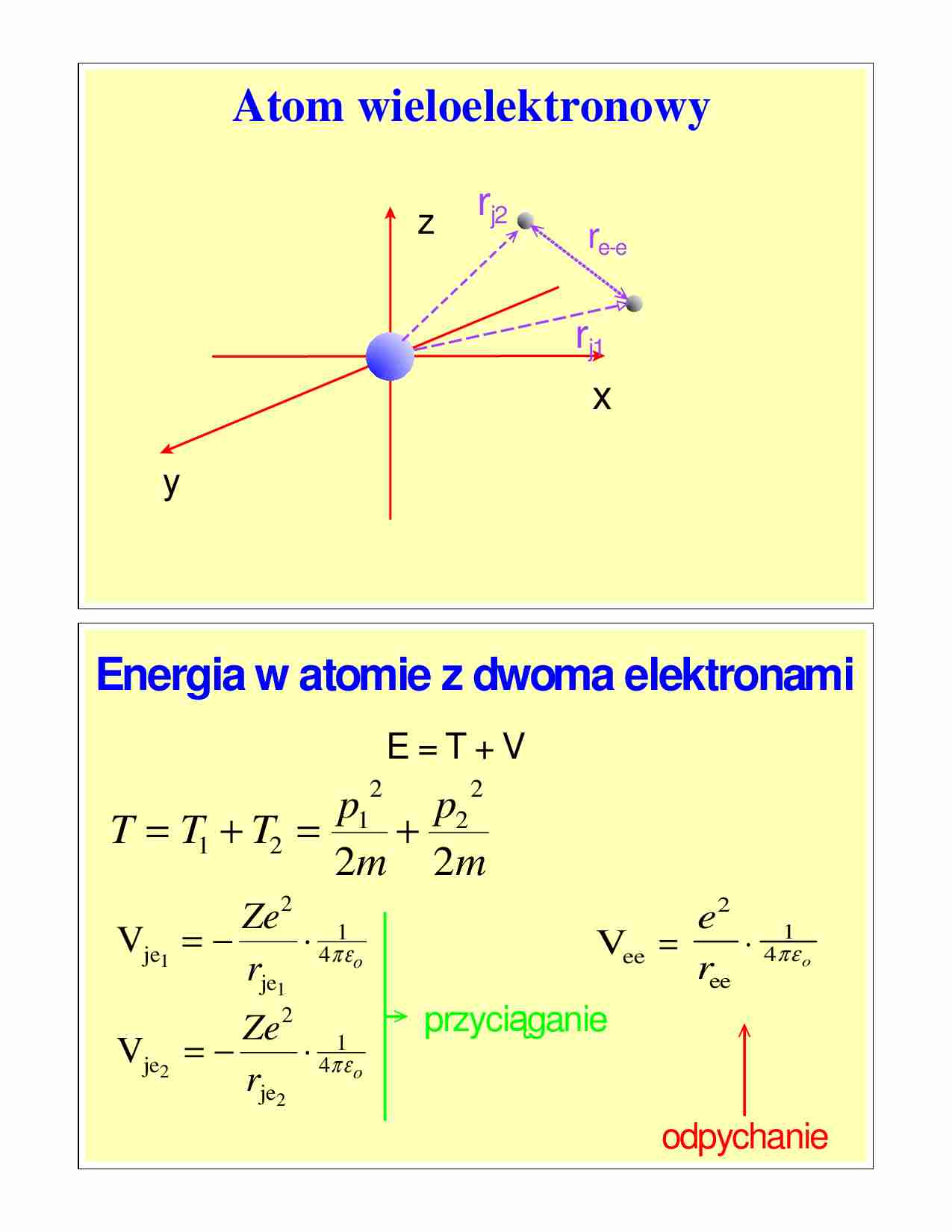
Atom wieloelektronowy
z
rj2
re-e
rj1
x
y
Energia w atomie z dwoma elektronami
E=T+V
2
1
2
p
p2
T = T1 + T2 =
+
2m 2 m
Vje1
Ze 2 1
=−
⋅ 4π ε o
rje1
Vje2
Ze 2 1
=−
⋅ 4π ε o
rje2
e2
Vee =
⋅
ree
przyciąganie
1
4π ε o
odpychanie
Energia w atomie z dwoma elektronami
1 Z
Z
1
V = 4πε o ⋅ e −
−
ree rje1 rje2
2
Człon odpowiadający oddziaływaniom pomiędzy
elektronami uniemoŜliwia rozwiązanie
równania Schrödingera
Energia w atomie z wieloma elektronami
1
H 1 oddziaływanie jądro-elektron
2
He 2 oddziaływania jądro-elektron
1 oddziaływanie elektron-elektron
4
Be 4 oddziaływania jądro-elektron
6 oddziaływanie elektron-elektron
11
Na 11 oddziaływań jądro-elektron
55 oddziaływań elektron-elektron
liczba oddziaływań w
atomie o liczbie
atomowej = Z
Z+
Z ⋅ ( Z − 1)
2
1
3
10
66
=
Z ⋅ ( Z + 1)
2
Energia całkowita w atomie
E=
1
2m
n
∑
i=1
p −
2
i
Ze2
4π ε o
n
∑
i= 1
1
ri
+
e2
4π ε o
n
∑ r1
i j = 1 ij
energia
oddziaływania oddziaływania
kinetyczna jadro-elektron elektron-elektron
elektronów
$ $ $
H = T+ V
$
HΨ = EΨ
MoŜna napisać równanie Schrödingera, ale nie ma
co marzyć o jego rozwiązaniu ...
Funkcja falowa atomu
wieloelektronowego
Funkcja falowa dla układu jądro + n elektronow
Q (x1, y1, z1, x2, y2, z2, ......xn, yn, zn),
jeśli uznać - jak w atomie wodoru - Ŝe jądro jest
nieruchome
jeśli uznać, Ŝe elektrony są niezaleŜne", to
moŜna przyjąć, Ŝe (w przybliŜeniu):
Q (x1, y1, z1, x2, y2, z2, ......xn, yn, zn) =
R1(x1, y1, z1)@R2(x2, y2, z2)@.....Rn(xn, yn, zn)
Takie przybliŜenie nosi nazwę
PRZYBLIśENIA JEDNOELEKTRONOWEGO
PrzybliŜenie jednoelektronowe"
ZałoŜenie:
- traktujemy osobno" kaŜdy z elektronów w
atomie, a jądro i pozostałe elektrony tworzą
uśrednione pole potencjału ...
... wobec tego kaŜdy elektron jest w sytuacji
podobnej, jak w atomie wodoru. Tylko pole
potencjału jest bardziej skomplikowane.
A z tym przecieŜ umieliśmy sobie poradzić ...
PrzybliŜenie jednoelektronowe (2)
Konsekwencje załoŜenia:
1.Energia atomu jest sumą energii elektronów:
n
E= ∑ E
i
i =1
2.Funkcja falowa całego atomu jest iloczynem
wszystkich jednoelektronowych" funkcji
falowych (orbitali elektronowych)
Q (x1, y1, z1, x2, y2, z2, ......xn, yn, zn) =
R1(x1, y1, z1)@R2(x2, y2, z2)@.....Rn(xn, yn, zn)
Sposób poszukiwania orbitali
jednoelektronowych
Metoda samouzgodnionego pola SCF
(Self-Consistent Field)
1.Określić sytuację wyjściową" i-tego elektronu w
średnim polu jądra i pozostałych elektronów.
2.Rozwiązać jednoelektronowe" równanie
Schrödingera, znaleźć orbital i energię i-tego el.
3.Korzystając z wyników dla i-tego elektronu
poprawić uśredniony" potencjał
4.Powtórzyć 1-3 dla elektronu i+1 i tak dalej aŜ
do n-tego.
Operację powtarzać aŜ do osiągnięcia
minimum energii...
Wyniki
Następuje częściowe zniesienie degeneracji energii:
w atomie wieloelektronowym:
Eel = En,l
w atomie wodoru:
Eel = En
E1s
(…)
… jest
minimalna, czyli wszystkie elektrony mają
minimalne (najniŜsze z moŜliwych) energie.
Wszystkie orbitale, które mają taką samą główną
liczbę kwantową n tworzą powłokę elektronową, a
orbitale z taką samą wartością n i l - podpowłokę
elektronową.
Reguły zapełniania powłok elektronowych
1.W stanie podstawowym poziomy energetyczne
są obsadzane według wzrastającej energii
2.W atomie nie mogą znajdować się równocześnie
dwa elektrony opisywane przez identyczną
czwórkę liczb n, l, m, ms (ZAKAZ PAULIEGO)
3.Wypadkowy spin elektronowy w atomie
przyjmuje maksymalną wartość
(REGUŁA HUNDA)
To trzeba umieć nawet będąc wyrwanym ze snu o 6 rano po
balu, który skończył się o 5.30 ....
Konfiguracje elektronowe pierwiastków
4p
4s
3p
3s
2p
2s
1s
3d
H
He
Li
Be
B
C
N
O
F
Ne
1s1
1s2
1s22s1
1s22s2
1s22s22p1
1s22s22p2
1s22s22p3…
... zobacz całą notatkę





Komentarze użytkowników (0)