To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
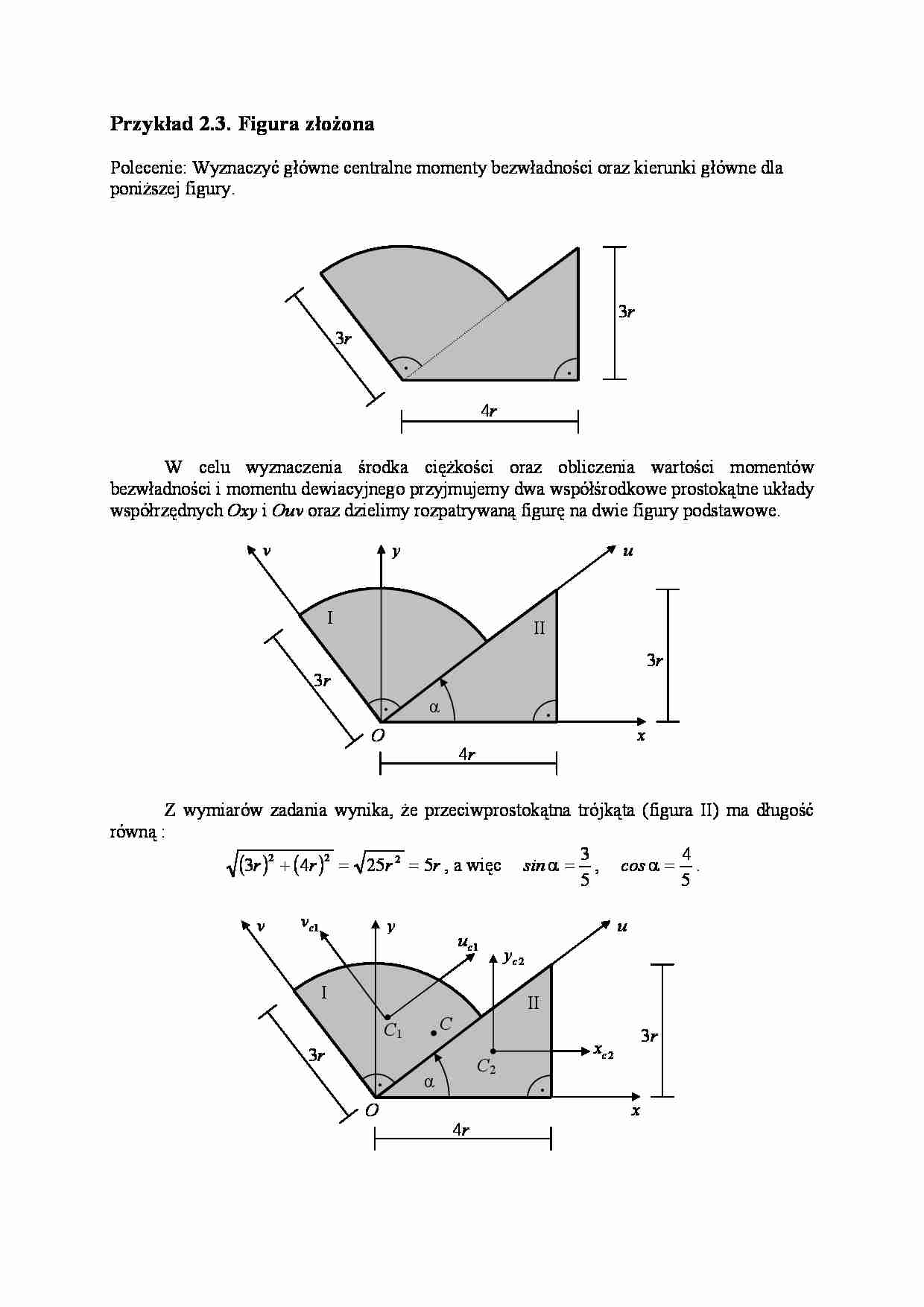


Przykład 2.3. Figura złożona
Polecenie: Wyznaczyć główne centralne momenty bezwładności oraz kierunki główne dla
poniższej figury.
3r
3r
·
·
4r
W celu wyznaczenia środka ciężkości oraz obliczenia wartości momentów
bezwładności i momentu dewiacyjnego przyjmujemy dwa współśrodkowe prostokątne układy
współrzędnych Oxy i Ouv oraz dzielimy rozpatrywaną figurę na dwie figury podstawowe.
v
y
u
I
II
3r
3r
·
α
·
O
x
4r
Z wymiarów zadania wynika, że przeciwprostokątna trójkąta (figura II) ma długość
równą :
(3r )2 + (4r )2 = 25r 2 = 5r , a więc sin α = 3 , cos α = 4 .
5
5
v
vc1
y
u c1
I
u
yc 2
II
C
C1
3r
·
O
C2
α
·
4r
3r
xc 2
x
Układ współrzędnych Ouv obrócony jest o kąt α względem układu Oxy. Współrzędne
dowolnego punktu spełniają zależności:
u = x cos α + y sin α
v = y cos α − x sin α.
Współrzędne środka ciężkości trójkąta (II figury) w układzie Oxy są równe:
~ = 2 ⋅4r = 8 r ,
~ = 1 ⋅ 3r = r
xc 2
yc 2
3
3
3
zaś w układzie Ouv przyjmują wartości:
8 4
3 41
~
~ = r⋅4 −8r⋅3 = −4r
uc 2 = r ⋅ + r ⋅ = r ,
vc 2
3 5
5 15
5 3 5
5
Obliczamy pola figur składowych i określamy współrzędne ich środków ciężkości w
układzie Ouv.
1
9
4 ⋅ 3r 4r
2
~
~ = 4 ⋅ 3r = 4r ,
A I = ⋅ π ⋅ (3r ) = πr 2 ,
u c1 =
vc1
=
,
4
4
π
π
3π
3π
41
1
~
~ =−4r.
A II = ⋅ 4r ⋅ 3r = 6r 2 ,
uc 2 = r ,
vc 2
15
5
2
Całkowite pole figury wynosi:
9
A = A I + A II = ⋅ πr 2 + 6r 2 = 13.0686r 2
4
Moment statyczny względem osi v wynosi:
9
41
⎛ 4r ⎞
~
~
S v = A I ⋅ u c1 + A II ⋅ u c 2 = πr 2 ⋅ ⎜ ⎟ + 6r 2 ⋅ r = 25.4r 3
4
15
⎝π ⎠
Moment statyczny względem osi u wynosi:
9
⎛ 4 ⎞
⎛ 4r ⎞
S u = A I ⋅ ~c1 + A II ⋅ ~c 2 = πr 2 ⋅ ⎜ ⎟ + 6r 2 ⋅ ⎜ − r ⎟ = 4.2r 3
v
v
4
⎝ 5 ⎠
⎝π ⎠
Współrzędne środka ciężkości rozpatrywanej figury w układzie Ouv wynoszą
odpowiednio:
3
S
25.4r 3
~
~ = S u = 4.2r
uc = v =
vc
= 1.9436r
oraz
= 0.3214r .
A 13.0686r 2
A 13.0686r 2
v
y
vc
I
u
uc
yc 2
II
C1
3r
·
C
C2
α
·
4r
3r
xc 2
x
Wyznaczymy momenty bezwładności i moment dewiacyjny dla obu figur składowych
w układzie osi Ouv. Dla pierwszej figury (ćwiartka koła) mamy
1
1
I
I
4
I
4
I u = I v = ⋅ π ⋅ (3r ) = 15.904r 4 ,
I uv = ⋅ (3r ) = 10.125r 4 .
16
8
Dla drugiej figury (trójkąt) obliczenia przeprowadzimy w układzie osi Oxy.
2
1
3
⋅ 4r ⋅ (3r ) = 9r 4
12
W celu wyznaczenia momentu bezwładności względem osi y figury II, przedstawimy
ją jako różnicę dwu figur, zgodnie z poniższym rysunkiem.
II
Ix =
y
y
3r
x
O
4r
x
O
4r
1
1
3
3
⋅ 3r ⋅ (4r ) − ⋅ 3r ⋅ (4r ) = 48r 4
3
12
Moment dewiacyjny figury II w układzie Oxy wyznaczymy korzystając z twierdzenia
Steinera
1
8
II
II
2
2
I xy = I xc yc + A II ⋅ ~c2 ⋅ ~c2 =
x y
⋅ (4r ) ⋅ (3r ) + 6r 2 ⋅ r ⋅ r = 18r 4 .
72
3
Momenty bezwładności i moment dewiacyjny figury II w obróconym układzie Ouv
wyznaczamy z zależności:
16
9
4 3
II
II
II
II
I u = I x cos 2 α + I y sin 2 α − 2 I xy sin α cos α = 9r 4 ⋅ + 48r 4 ⋅ − 18r 4 ⋅ ⋅ = 5.76r 4
25
25
5 5
16
9
4 3
II
II
II
II
I v = I y cos 2 α + I x sin 2 α + 2 I xy sin α cos α = 48r 4 ⋅ + 9r 4 ⋅ + 18r 4 ⋅ ⋅ = 51.24r 4
25
(…)
… na dwa trójkąty prostokątne, których boki przyprostokątne są równoległe do osi
układu Ouv zgodnie z poniższym rysunkiem.
3
4
sin α = , cos α =
5
5
3 12
h = 4r ⋅ sin α = 4r ⋅ = r
5 5
4 16
b2 = 4r ⋅ cos α = 4r ⋅ = r
5 5
3
b3 = 3r ⋅ sin α = 3r ⋅
b3
y
v
b2
vc 2
u
vc 3
· ·
III
u c3
h
3r
C3
uc2
II
C2
α
3 9
= r
5 5
x
4r
Pola powierzchni figury II i III oraz współrzędne ich środków ciężkości w obróconym
układzie Ouv…
... zobacz całą notatkę






Komentarze użytkowników (0)