To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
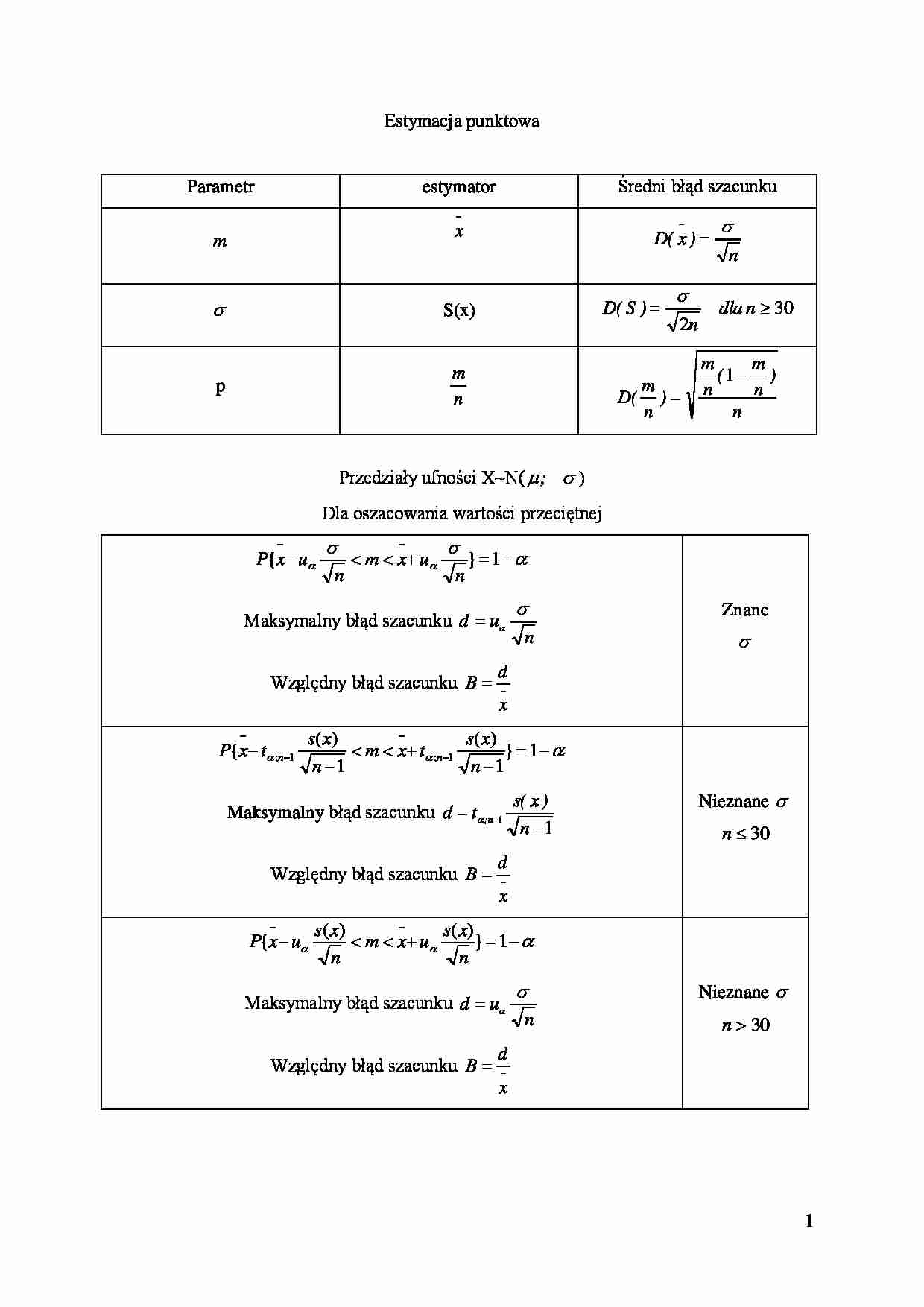


Estymacja punktowa
Parametr
Średni błąd szacunku
estymator
x
m
D( x )
p
D( S )
S(x)
m
n
2n
m
D( )
n
n
dla n 30
m
m
(1 )
n
n
n
Przedziały ufności X~N( ; )
Dla oszacowania wartości przeciętnej
P{x u
n
m x u
n
} 1
Maksymalny błąd szacunku d u
Względny błąd szacunku B
n
Znane
d
x
P{x t ;n1
s ( x)
s ( x)
m x t ;n1
} 1
n 1
n 1
Maksymalny błąd szacunku d t ;n1
Względny błąd szacunku B
s( x )
n 1
Nieznane
n 30
d
x
P{x u
s ( x)
s ( x)
m x u
} 1
n
n
Maksymalny błąd szacunku d u
Względny błąd szacunku B
n
Nieznane
n 30
d
x
1
Dla oszacowania wartości wskaźnika struktury
P{
m
m
(1 )
n
n p m u
n
n
m
u
n
m
m
(1 )
n
n } 1
n
m
m
(1 )
n
n
n
Maksymalny błąd szacunku d u
n100
d
m
n
Względny błąd szacunku B
Dla oszacowania wartości wariancji
P{
ns 2 ( x)
2
2
P{s( x) u
;n 1
ns 2 ( x)
2
2
} 1
n 30
1 ;n 1
2
s ( x)
s ( x)
s( x) u
} 1
2n
2n
n 30
Dla oszacowania wartości współczynnika korelacji liniowej Pearsona
e 2 z1 1
e 2 z2 1
P{ 2 z1
xy 221 } 1
e 1
e 1
z1 z
u
n3
P{rxy u
z2 z
;
1 rxy
u
n3
2
n
xy rxy u
1 1 rxy
z ln
2 1 rxy
;
1 rxy
n 120
2
n
} 1
n 120
Dla oszacowania wartości współczynnika liniowej funkcji regresji
P{ak t ;n2
s(u )
n
(x
i 1
P{ak u
i
i 1
( xi x) 2
i 1
n
(x
x) 2
s(u )
n
s(u )
k ak t ;n2
k ak u
i
x) 2
s(u )
n
} 1
( xi x) 2
} 1
n 30
k = 0, 1
n 30
k = 0, 1
i 1
2
Przyjmuje się, że jeżeli względny błąd szacunku:
B 0,05 - to oszacowanie charakteryzuje się dużą precyzją
0,05 B 0,1- to uogólnienia wyników z próby na całą populację należy dokonywać
z ostrożnością
0,05 B 0,1- to nie należy przeprowadzać żadnych uogólnień
Niezbędna liczebność próby dla oszacowania wartości przeciętnej z maksymalnym błędem
szacunku nie większym niż ustalone d
u 2
d2
2
Znane
nmin
Nieznane
nmin
2
u s 2 ( x )
d2
Niezbędna liczebność próby dla oszacowania wskaźnika struktury z maksymalnym błędem
szacunku nie większym niż ustalone d
nmin
u
2
m
m
(1 )
n
n
2
d
2
Dla nieznanego rzędu wielkości wskaźnika struktury
nmin
u
2
4d
3
... zobacz całą notatkę






Komentarze użytkowników (0)