To tylko jedna z 4 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
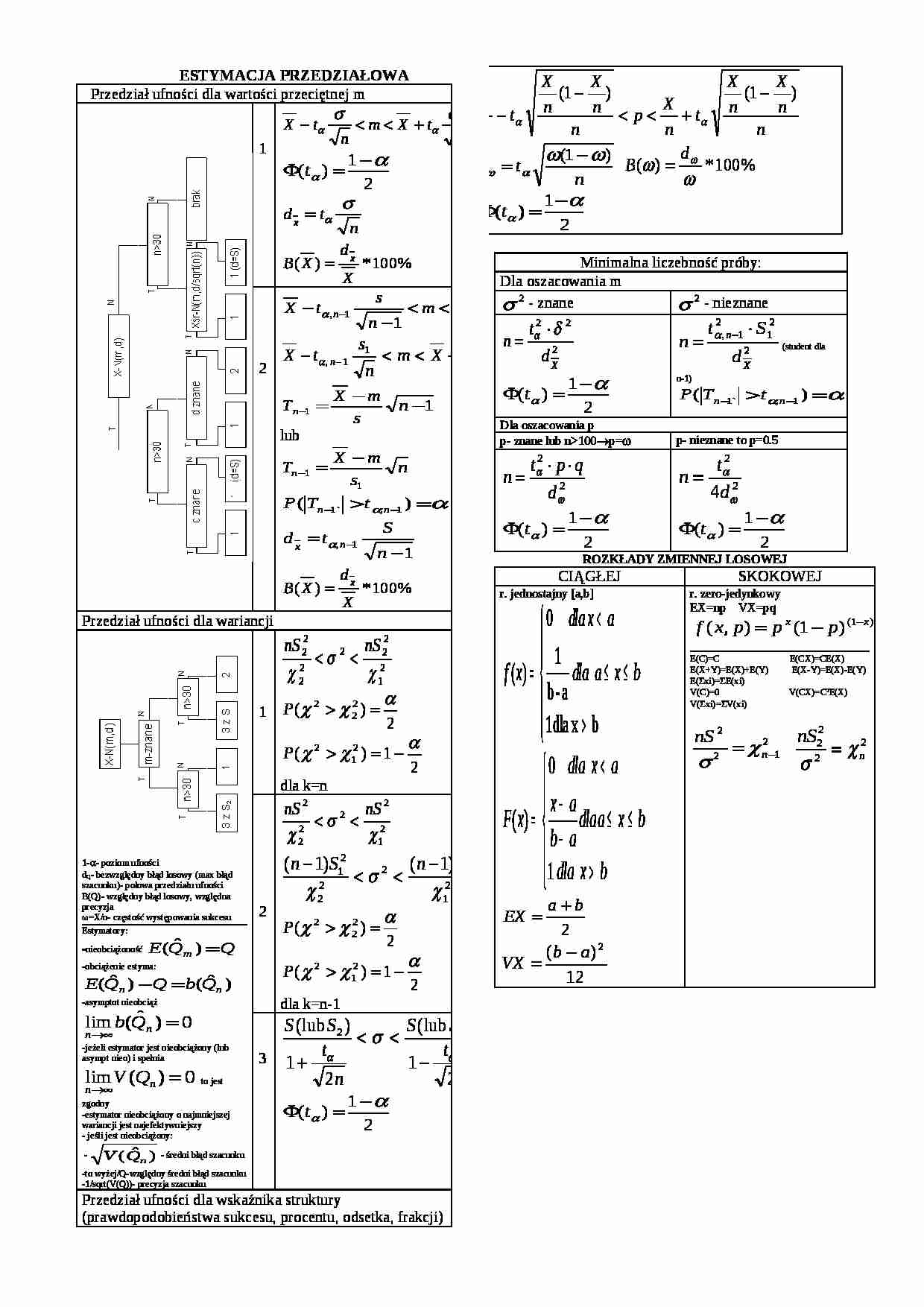


ESTYMACJA PRZEDZIAŁOWA Przedział ufności dla wartości przeciętnej m
1
2
lub
Przedział ufności dla wariancji
1-α- poziom ufności
d Q - bezwzględny błąd losowy (max błąd szacunku)- połowa przedziału ufności
B(Q)- wzgłędny błąd losowy, względna precyzja
ω=X/n- częstość występowania sukcesu
Estymatory:
-nieobciążoność -obciążenie estyma: -asymptot nieobciąż -jeżeli estymator jest nieobciążony (lub asympt nieo) i spełnia to jest zgodny
-estymator nieobciążony o najmniejszej wariancji jest najefektywniejszy
- jeśli jest nieobciążony:
- - średni błąd szacunku
-to wyżej/Q-względny średni błąd szacunku
-1/sqrt(V(Q))- precyzja szacunku 1
dla k=n
2
dla k=n-1
3
Przedział ufności dla wskaźnika struktury (prawdopodobieństwa sukcesu, procentu, odsetka, frakcji)
Minimalna liczebność próby:
Dla oszacowania m
- znane
- nieznane
(student dla n-1) Dla oszacowania p
p- znane lub n100→p=ω
p- nieznane to p=0.5
ROZKŁADY ZMIENNEJ LOSOWEJ CIĄGŁEJ
SKOKOWEJ
r. jednostajny [a,b] r. zero-jedynkowy
EX=np VX=pq
E(C)=C E(CX)=CE(X)
E(X+Y)=E(X)+E(Y) E(X-Y)=E(X)-E(Y)
E(Σxi)=ΣE(xi)
V(C)=0 V(CX)=C 2 E(X)
V(Σxi)=ΣV(xi)
r. wykładniczy EX= VX= r. dwumianowy
EX=np VX=npq
gdy p100- przybliżamy r. Poissona
gdy n30- przybliżamy r. normalnym X-N(np., ) r. normalny
EX=m VX= r. Poissona
EX=m VX=m
r. chi-kwadrat
dla k30⇒ r. geometryczny
r. studenta
T-N(0,1)
r. hipergeometryczny
N-liczba el. W populacji
R-liczba el majacych wyróżnioną cechę w populacji
... zobacz całą notatkę






Komentarze użytkowników (0)