To tylko jedna z 10 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
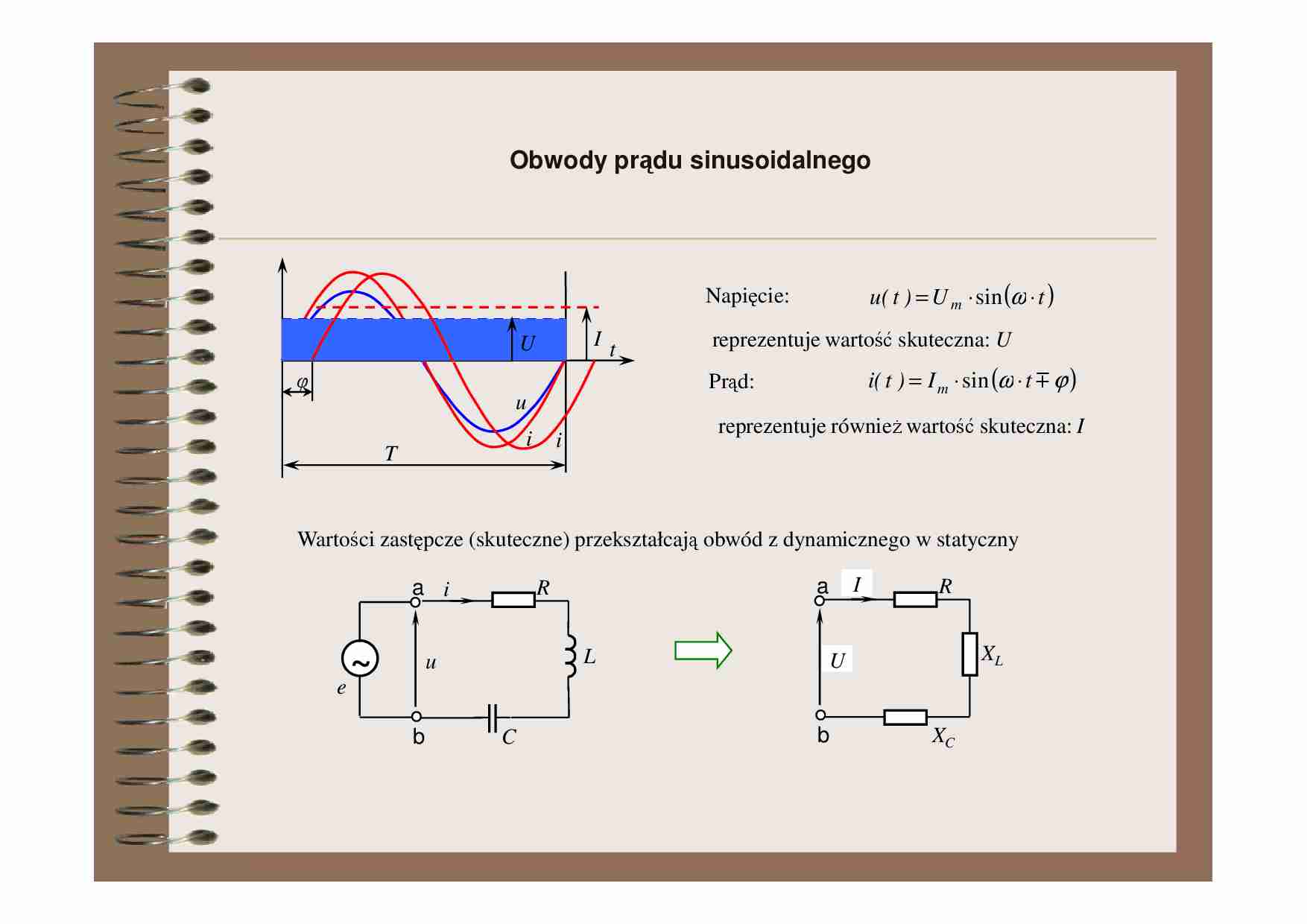

Obwody prądu sinusoidalnego
u( t ) = U m ⋅ sin (ω ⋅ t )
Napięcie:
I
U
t
reprezentuje wartość skuteczna: U
i( t ) = I m ⋅ sin (ω ⋅ t m ϕ )
Prąd:
φ
u
i
T
reprezentuje równieŜ wartość skuteczna: I
i
Wartości zastępcze (skuteczne) przekształcają obwód z dynamicznego w statyczny
a i
e
~
L
u
b
a iI
R
C
R
XL
u
U
b
XC
Dwójnik R, L
a
I
RozwaŜany obwód w dziedzinie czasu opisuje zaleŜność:
R
UR
U
u = R ⋅i + L ⋅
L
UL
b
U
φ+
UL
UR
I
di
= uR + uL
dt
UR = R ⋅ I
UL = X L ⋅ I = ω ⋅ L ⋅ I
2
2
U = UR +UL = Z ⋅ I
XL
R
U j ⋅arc tg
I = ⋅e
Z
2
Z = R2 + X L
Zamiast sum geometrycznych moŜna uŜyć zapisu symbolicznego – liczba zespolona:
z = a + j ⋅b
Z = R+ j⋅X
z = Z ⋅ (cos(ϕ ) + j ⋅ sin (ϕ ))
R = Z ⋅ cos(ϕ ) oraz
z = Z ⋅ e j ⋅ϕ
2
Z = R2 + X L
X L = Z ⋅ sin (ϕ )
U
ω⋅L
tg(ϕ ) = L =
UR
R
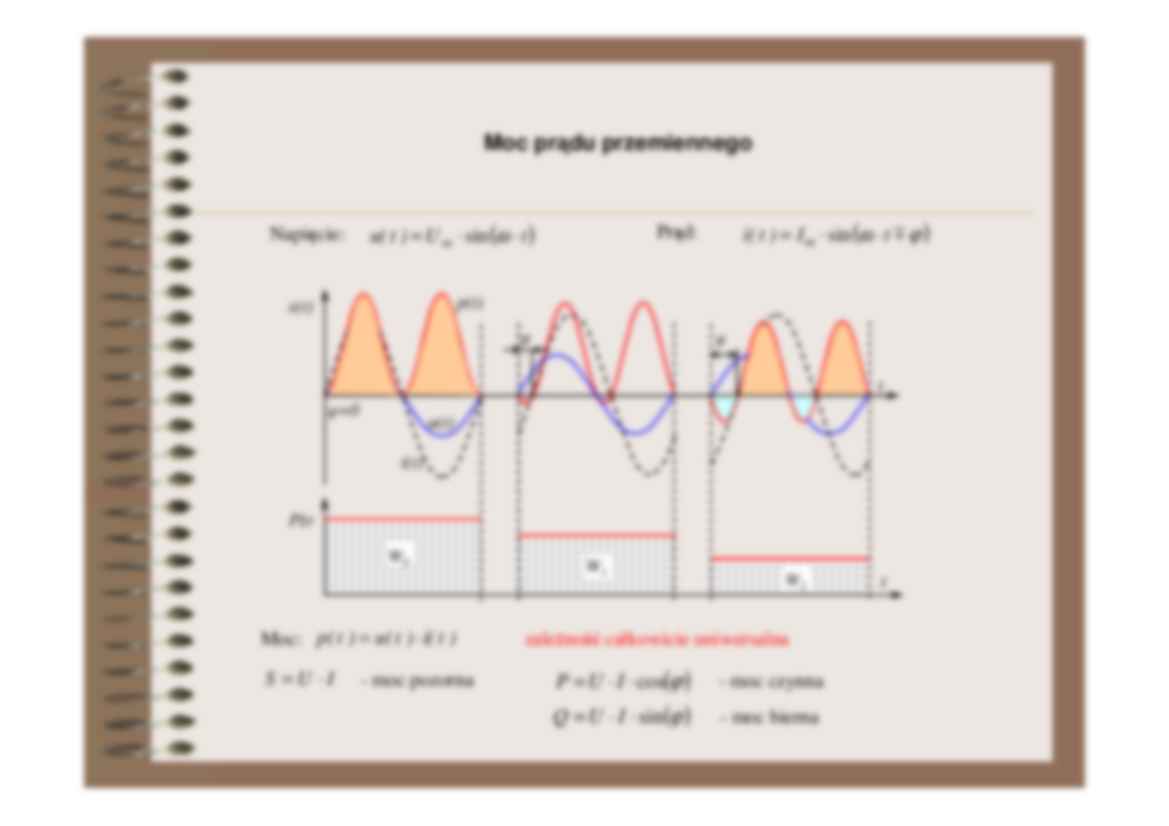
Moc prądu przemiennego
Napięcie:
u( t ) = U m ⋅ sin (ω ⋅ t )
i( t ) = I m ⋅ sin (ω ⋅ t m ϕ )
Prąd:
p(t)
x(t)
φ
φ
t
φ=0
u(t)
i(t)
Pśr
W0
Moc: p( t ) = u( t ) ⋅ i( t )
S =U ⋅I
- moc pozorna
W1
W2
zaleŜność całkowicie uniwersalna
P = U ⋅ I ⋅ cos(ϕ )
Q = U ⋅ I ⋅ sin (ϕ )
- moc czynna
- moc bierna
t
Dwójnik R, C
a I
U
RozwaŜany obwód w dziedzinie czasu opisuje zaleŜność:
R
UR
UC
u = R ⋅i +
C
1
⋅ ∫ i ⋅ dt = u R + u C
C
b
UR = R ⋅ I
UR
I
UC = − X C ⋅ I = −
φU
UC
1
⋅I
ω ⋅C
2
Z = R2 + X C
XC
R
U j ⋅arc tg
I = ⋅e
Z
Dwójnik szeregowy R, L, C
a
RozwaŜany obwód w dziedzinie czasu opisuje zaleŜność:
R
I
UR
UL
U
u = R ⋅i + L⋅
L
di 1
+ ⋅ ∫ i ⋅ dt = u R + u L + uC
dt C
UC
b
C
π I
π
u = U m ⋅ sin (ω ⋅ t + ϕ ) = R ⋅ I m ⋅ sin (ω ⋅ t ) + ω ⋅ L ⋅ I m ⋅ sin ω ⋅ t + + m ⋅ sin ω ⋅ t −
2 ω ⋅C
2
U X = U L − UC
UL
U
UC
φ+
I UR
Moc (energia):
Wniosek:
X
U j ⋅arc tg R
I = ⋅e
Z
Z = R + j ⋅ (X L − X C )
U2
P = U ⋅ I ⋅ cos(ϕ ) = R ⋅ I = R ⋅ 2
Z
2
ze źródeł napięciowych maksymalną energię moŜna przesłać (przetworzyć)
wówczas, gdy obwód posiada charakter rezystancyjny.
Dwójnik równoległy R, L, C
a
I
IR
IL
IC
R
L
C
U
b
i = I m ⋅ sin (ω ⋅ t + ψ ) =
RozwaŜany obwód w dziedzinie czasu opisuje zaleŜność:
i=
u
du 1
+C⋅
+ ⋅ ∫ u ⋅ dt = iR + iC + iL
R
dt L
Um
π U
π
⋅ sin (ω ⋅ t ) + ω ⋅ C ⋅ U m ⋅ sin ω ⋅ t + + m ⋅ sin ω ⋅ t −
R
2 ω⋅L
2
IC
IR =
U j0
⋅e
R
IC = ω ⋅ C ⋅U ⋅ e
U
φ+
IR IL
I
π
2
π
−j
U
IL =
⋅e 2
ω⋅L
2
Moc (energia):
j
2
P = U ⋅ I ⋅ cos(ϕ ) = R ⋅ I R = U
R
I X = I L − IC
2
2
I = IR + I X
Rezonanse w obwodach elektrycznych
Zjawisko rezonansu przedstawia taki stan pracy obwodu elektrycznego,
przy którym reaktancja wypadkowa obwodu lub susceptancja
wypadkowa jest równa zeru.
Rezonans napięć
a
U
b
lub kompensacja szeregowa:
R
I
UR
UL
U = U R + U L + U C = [R + j ⋅ ( X L − X C )] ⋅ I
L
UC
X = X L − XC = 0
X L = XC
C
fs =
UL
I
UC
UR =U
ω⋅L =
1
ω ⋅C
1
2 ⋅π ⋅ L ⋅ C
Rs = R
I = I max =
U
R
Rezonans prądów
a I
IR
IL
L
C
lub kompensacja równoległa:
IC
U
R
1
1
1
⋅ U = [G + j ⋅ (BC − BL
... zobacz całą notatkę






Komentarze użytkowników (0)