Temat: regresja liniowa wielu zmiennych cz. 2 – pełna weryfikacja modelu ostatecznego
Cele:
−
Poznanie możliwości zastosowania metody analizy regresji w odniesieniu do badania zjawisk ekonomicznych, gospodarczych i demograficznych.
−
Zapoznanie się z zasadami doboru danych do modelu regresji oraz podstawowymi źródłami ich pozyskiwania.
−
Zdobycie umiejętności modelowania zależności miedzy zjawiskami – zapisanie modelu regresji w pełnej postaci, weryfikacja modelu i interpretacja oszacowanej zależności.
−
Zdobycie umiejętności tworzenia prognoz na podstawie modelu – założenia, które muszą być spełnione przy prognozowaniu; tworzenie prognoz punktowych i przedziałowych.
−
Zdobycie umiejętności praktycznego wykorzystania metody analizy regresji w badaniach oraz interpretacji otrzymanych wyników językiem „menedżerskim”.
4. Badanie autokorelacji składnika losowego
Zgodnie z założeniami modelu regresji składniki losowe (błędy) odpowiadające kolejnym obserwacjom powinny być od siebie niezależne, czyli nie powinna zachodzić między nimi korelacja niezależnie od tego, jaka jest pozycja błędu w ciągu obserwacji. Błąd na pozycji i nie jest skorelowany z błędami na pozycjach i‐1, i‐2, i‐3 ...
Do badania autokorelacji składnika losowego stosuje się test Durbina‐Watsona. Wartość statystyki testowej (dobl – D‐W), wyznaczanej ze wzoru:
ekonometria, laboratoria VI – zarządzanie, studia stacjonarne I stopnia, rok II
Temat: regresja liniowa wielu zmiennych cz. 2 – pełna weryfikacja modelu ostatecznego Cele:
− Poznanie możliwości zastosowania metody analizy regresji w odniesieniu do badania
zjawisk ekonomicznych, gospodarczych i demograficznych.
− Zapoznanie się z zasadami doboru danych do modelu regresji oraz podstawowymi
źródłami ich pozyskiwania.
− Zdobycie umiejętności modelowania zależności miedzy zjawiskami – zapisanie modelu
regresji w pełnej postaci, weryfikacja modelu i interpretacja oszacowanej zależności.
− Zdobycie umiejętności tworzenia prognoz na podstawie modelu – założenia, które muszą
być spełnione przy prognozowaniu; tworzenie prognoz punktowych i przedziałowych.
− Zdobycie umiejętności praktycznego wykorzystania metody analizy regresji w badaniach
oraz interpretacji otrzymanych wyników językiem „menedżerskim”. Materiały:
− skrypt: „Statystyka i ekonometria” pod redakcją prof. Z. Łuckiego, Uczelniane
Wydawnictwa Naukowo‐Dydaktyczne AGH, Kraków 2008,
− wykłady, − zadania i materiały zawarte w instrukcji. PRZEBIEG LABORATORIÓW
Badanie wyrazistości modelu
Dla modelu oblicza się współczynnik wyrazistości dany wzorem:
s( y)W
=
100 %obly
Współczynnik informuje, jaki procent średniej arytmetycznej zmiennej objaśnianej modelu (Y) stanowi błąd resztowy (s(y) ‐ odchylenie standardowe reszt). Im mniejszą wartość przyjmuje współczynnik, tym bardziej „wyraźnie” kształt smugi punktów, którą tworzy wykres danych empirycznych („scatterplot”), przypomina kształt teoretycznej linii regresji (w przypadku regresji dwóch zmiennych). W związku z tym im mniejsze wartości przyjmuje współczynnik W, tym model jest lepiej dopasowany do danych empirycznych.
Procedura badania wyrazistości modelu:
− określenie się maksymalną wartość W*, po której przekroczeniu uznajemy model za mało
wyrazisty – przyjmujemy krytyczna wartość współczynnika W*=30%,
− wyznaczenie na podstawie danych empirycznych wartość współczynnika zmienności W
zgodnie ze wzorem podanym
(…)
… z rozkładu normalnego – statystyka testowa z:
m 1
−
n 2
z=
↔ zα
m⎛ m⎞
⎜1 − ⎟
n⎝
n⎠
n −1
Analogiczny obszar odrzucenia wyznaczony w oparciu o zmienną z.
Asymetria składnika losowego może wynikać z wadliwego wyboru klasy modelu
ekonometrycznego oraz z przyjęcia niewłaściwej postaci analitycznej modelu.
2. Badanie losowości składnika losowego
Prawidłowo zbudowany model powinien zapewniać losowe kształtowanie się reszt, na
podstawie czego wnioskujemy o losowości składnika losowego.
Sprowadza się to do postawienia pary hipotez:
H 0 : ξ jest skadnikiem czysto losowym
H1 : ξ nie jest losowy
ekonometria, laboratoria VI – zarządzanie, studia stacjonarne I stopnia, rok II
Posługujemy się testem serii:
Wyróżniamy dwa rodzaje elementów:
A – wartości ei<0(reszty ujemne)
B…
… dotyczące normalności rozkładu
składnika losowego (reszt). Zgodnie z założeniami, reszty powinny mieć rozkład normalny
o wartości średniej równej zero – N(0, σ).
Histogram for RESIDUALS
16
frequency
12
8
4
0
-8
-5
-2
1
4
7
10
RESIDUALS
Do badania normalności rozkładu składnika losowego można zastosować test χ2 lub test
λ‐Kołmogorowa.
4. Badanie autokorelacji składnika…
… losowego stosuje się test Durbina‐Watsona. Wartość
statystyki testowej (dobl – D‐W), wyznaczanej ze wzoru:
n
DW =
∑ (e
i=2
i
− ei −1 ) 2
n
∑e
i =1
2
i
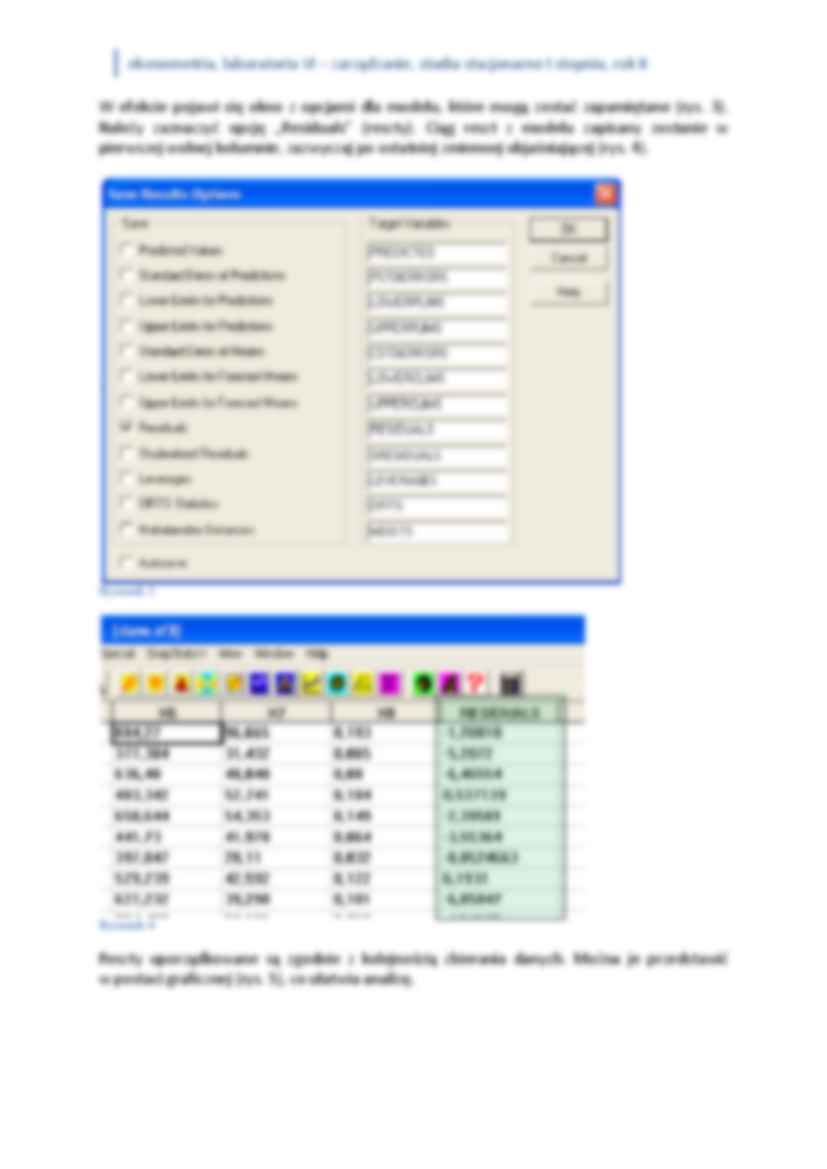
można odczytać z wydruku analizy regresji (rys. 4).
ekonometria, laboratoria VI – zarządzanie, studia stacjonarne I stopnia, rok II
Rysunek 6
Na podstawie tablic Durbina‐Watsona wyznaczamy dwie wartości krytyczne: dL i dU…
... zobacz całą notatkę





Komentarze użytkowników (0)