To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
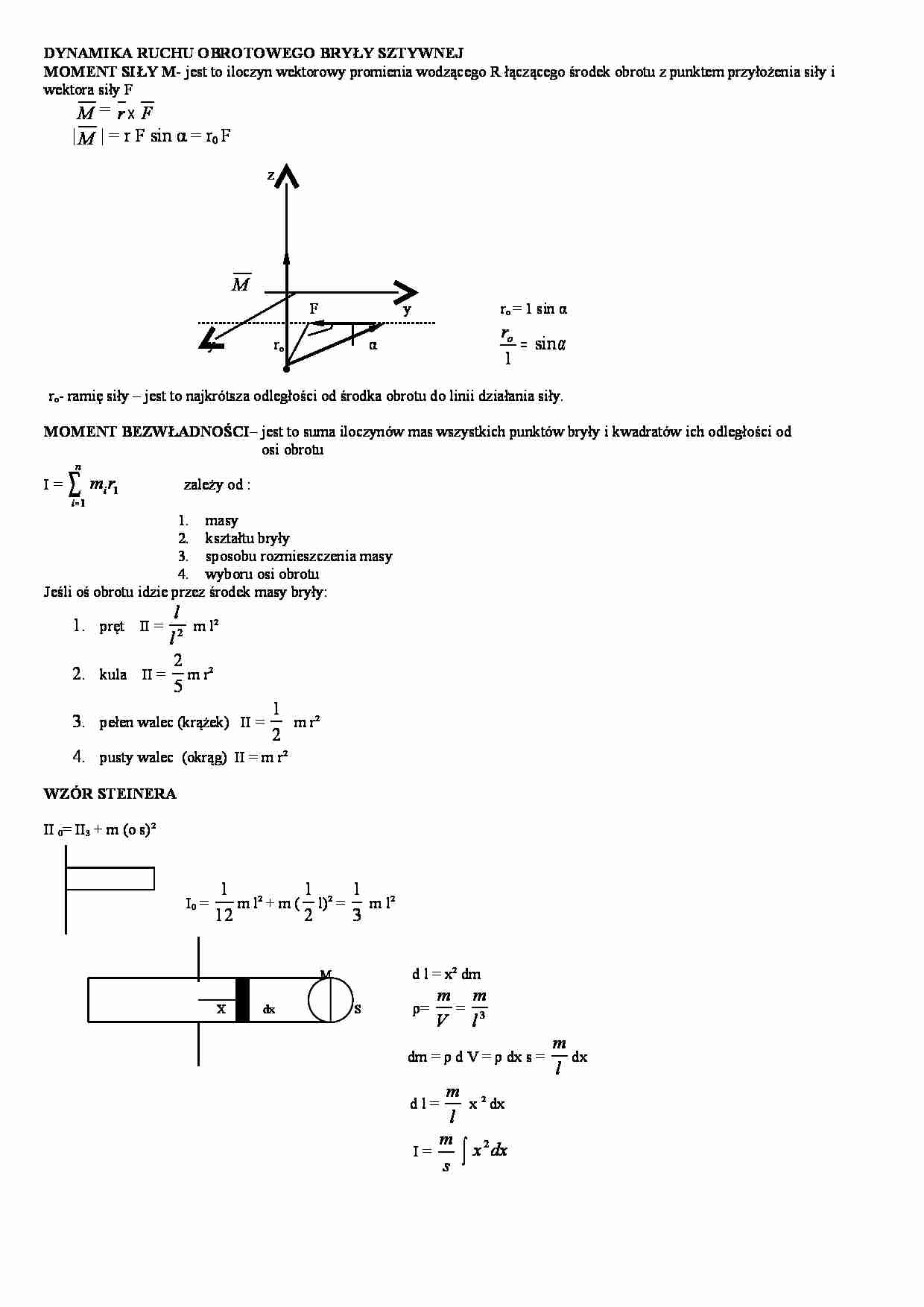


DYNAMIKA RUCHU OBROTOWEGO BRYŁY SZTYWNEJ MOMENT SIŁY M - jest to iloczyn wektorowy promienia wodzącego R łączącego środek obrotu z punktem przyłożenia siły i wektora siły F M = F r × | M | = r F sin α = r0 F z M F y ro = 1 sin α y ro α α sin 1 = o r ro- ramię siły – jest to najkrótsza odległości od środka obrotu do linii działania siły. MOMENT BEZWŁADNOŚCI – jest to suma iloczynów mas wszystkich punktów bryły i kwadratów ich odległości od osi obrotu I = 1 1 r m n i i ∑ = zależy od : 1. masy 2. kształtu bryły 3. sposobu rozmieszczenia masy 4. wyboru osi obrotu Jeśli oś obrotu idzie przez środek masy bryły: 1. pręt II = 2 l l m l2 2. kula II = 5 2 m r2 3. pełen walec (krążek) II = 2 1 m r2 4. pusty walec (okrąg) II = m r2 WZÓR STEINERA II 0= II3 + m (o s)2 I0 = 12 1 m l2 + m ( 2 1 l)2 = 3 1 m l2 M d l = x2 dm X dx S ρ= V m = 3 l m dm = ρ d V = ρ dx s = l m dx d l = l m x 2 dx I = s m ∫ dx x 2 A) przez środek 2 1 −
(…)
… nie obraca się lub obraca się ruchem jednostajnym jeżeli nie działa na nią żaden moment siły lub momenty sił się
równoważą
n
∑
i= 1
Mi = 0
M1 + M 2 + = 0
W spoczynku
n
∑
i= 1
n
Mi = 0
;
∑
i= 1
Fi = 0
2. Jeżeli na bryłę nie działa wypadkowy moment siły, to nadaje on bryle przyśpieszenie kątowe
do tego momentu a odwrotnie proporcjonalne do momentu bezwładności
M
I
(1)
(2)
M = Iε = I
(3)
3.
ε =
M dt = d l
ε…
... zobacz całą notatkę






Komentarze użytkowników (0)