To tylko jedna z 7 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
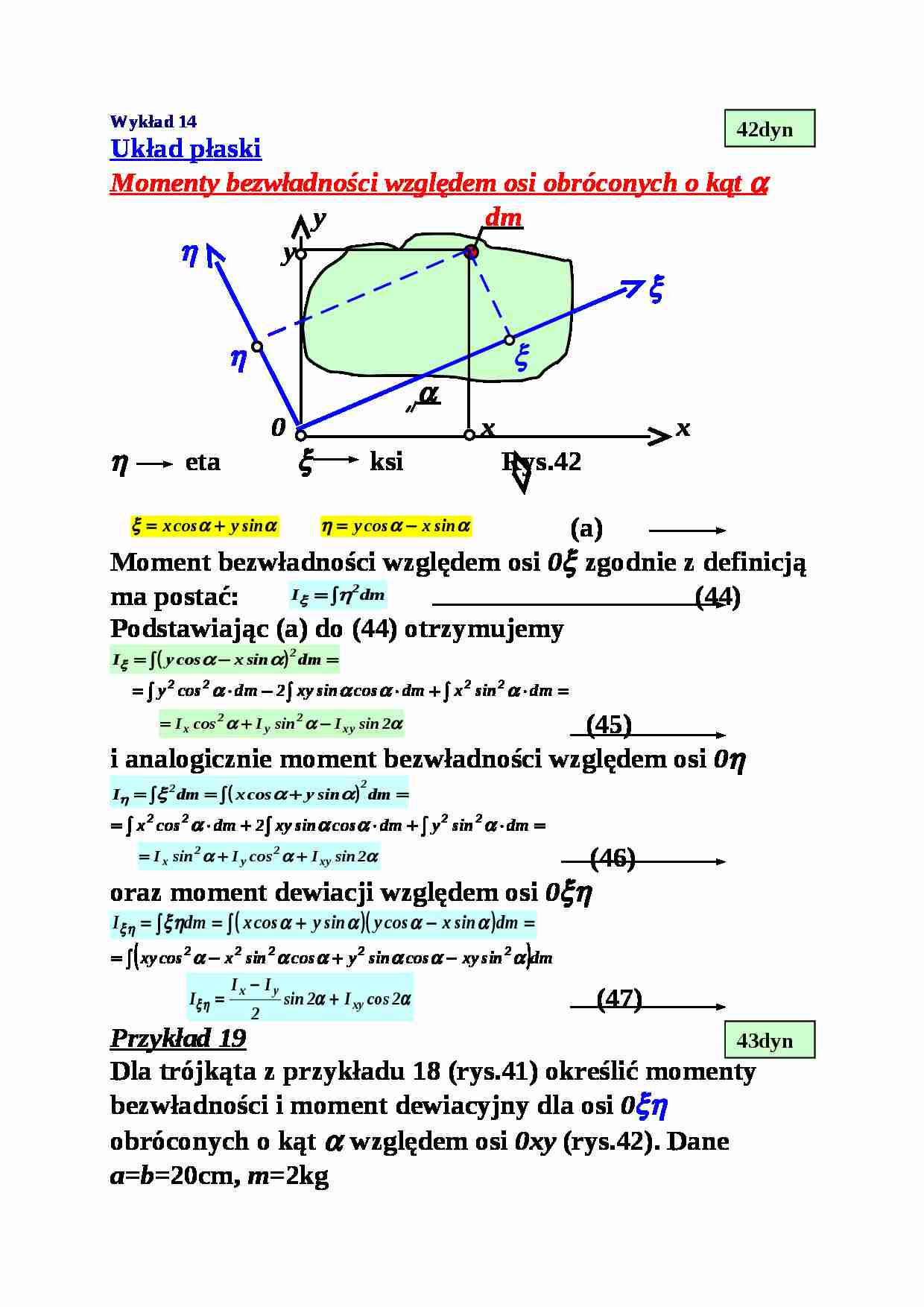


Wykład 14 Układ płaski Momenty bezwładności względem osi obróconych o kąt α y dm η y ξ η ξ α 0 x x η eta ξ ksi Rys.42 (a) Moment bezwładności względem osi 0 ξ zgodnie z definicją ma postać: (44) Podstawiając (a) do (44) otrzymujemy (45) i analogicznie moment bezwładności względem osi 0 η (46) oraz moment dewiacji względem osi 0 ξ η (47) Przykład 19 Dla trójkąta z przykładu 18 (rys.41) określić momenty bezwładności i moment dewiacyjny dla osi 0 ξ η obróconych o kąt α względem osi 0xy (rys.42). Dane a = b =20cm, m =2kg Rozwiązanie y η ξ α = 25 0 α 0 x Rys.42 Z przykładu 18 mamy, że (48) Określenie momentu dewiacji względem osi 0xy (49) Podstawiając otrzymane wzory do (45), (4 6), (47) otrzymujemy Dla α = 45 0 osie główne Osie główne Główne momenty bezwładności (b) Z równania (b) otrzymujemy równanie na kąt α 0 , który określa położenie głównych osi bezwładności w stosunku do układu 0xy (rys.42) (50) Po podstawieniu wartości kąta α 0 (50) do równań (45) i (46) otrzymujemy wzór na obliczanie głównych momentów bezwładności (51) (51) Przypadek gdy I x = I 1 , I y = I 2 , I xy = 0, czyli gdy osie 0xy są osiami głównymi wtedy y η
(…)
… (52)
(c)
to otrzymamy
(53)
Przykład 20
Określić wartość pracy siły ciężkości jeżeli masa m = 5 kg
przemieściła się z poziomu h1 = 7 m na poziom h2 = 3 m.
Dane: = 0 m/s, opór ośrodka pominąć.
Rozwiązanie Px= 0, Py = 0, Pz = -mg
z h1 P
h2 m
P = mg
0 y Z wzoru (52) Praca sił przyłożonych do ciała sztywnego Praca sił zewnętrznych w ruchu postępowym dri ai ai = aj = a
drj aj Pi dri = drj = dr
rj ri
Pj 0 Rys.45
Praca elementarna siły Pi Praca elementarna wszystkich sił zewnętrznych działających na ciało Praca sił zewnętrznych na przesunięciu skończonym AB
(54)
Praca sił zewnętrznych w ruchu obrotowym
A
ri Pin A dri Pin
Pit Piz Pit
Miz ri z dφ
Rys.46 Pi = Pin + Pit + Piz (55)
Praca sił wewnętrznych
Pojęcie mocy
Moc siły praca wykonana przez siłę w ciągu jednostki czasu
Moc średnia w przedziale czasu…
…
(59)
dżul (J) jednostka energii kinetycznej Energia kinetyczna w ruchu postępowym Wszystkie punkty mają tę samą prędkość Vi =Vi+1 = V
gdzie Energia kinetyczna ciała sztywnego w ruchu obrotowym
ω l V = ωr l
V ω m
r r
dm dm
Rys.47
Energia kinetyczna elementu ciała dm Energia kinetyczna całego ciała
(60)
gdzie moment bezwładności względem osi l
42dyn
43dyn
44dyn
45dyn
46dyn
47dyn
48dyn
…
… Δt
(56)
Wartość mocy chwilowej siły
(57)
Z wzoru (57) mamy
(58)
Z definicji podstawiając to do (57) mamy
(59)
Moc siły jest to iloczyn skalarny wektora siły P i wektora prędkości V punktu jej przyłożenia.
W prostokątnym układzie
(60)
Ze wzoru (59) wynika, że V
P α
Energia kinetyczna
Energia kinetyczna układu punktów materialnych jest równa sumie energii kinetycznej wszystkich punktów materialnych…
... zobacz całą notatkę






Komentarze użytkowników (0)