To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
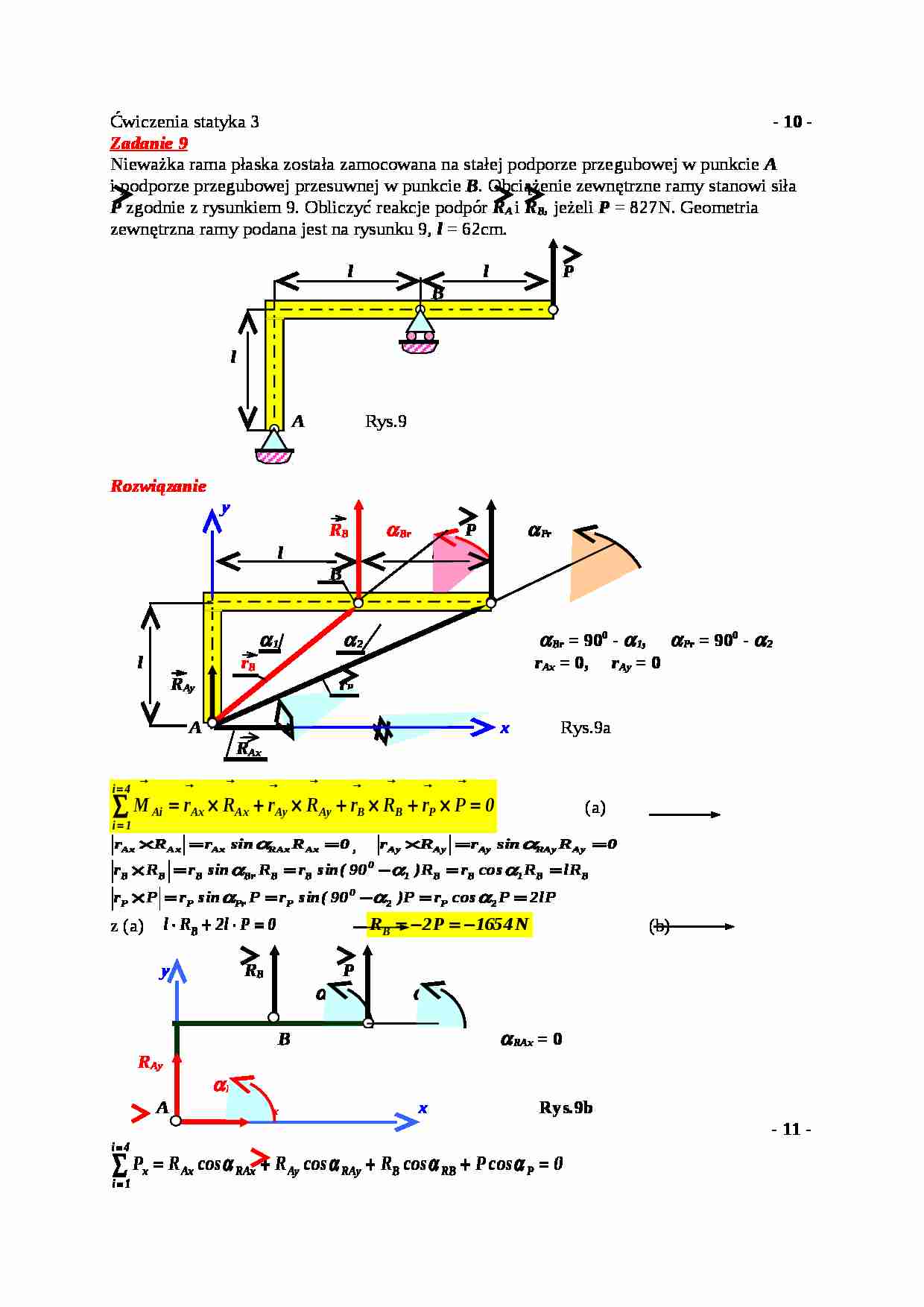


Ćwiczenia statyka 3 - 10 - Zadanie 9 Nieważka rama płaska została zamocowana na stałej podporze przegubowej w punkcie A i podporze przegubowej przesuwnej w punkcie B . Obciążenie zewnętrzne ramy stanowi siła
P zgodnie z rysunkiem 9. Obliczyć reakcje podpór R A i R B , jeżeli P = 827N. Geometria zewnętrzna ramy podana jest na rysunku 9, l = 62cm.
l l P B l A Rys.9
Rozwiązanie y R B α Br P α Pr l l B α 1 α 2 α Br = 90 0 - α 1 , α Pr = 90 0 - α 2 l r B r Ax = 0, r Ay = 0 R Ay r P A x Rys.9a
R Ax (a)
, z (a) (b)
y R B P α RB α P B α RAx = 0 R Ay α RAy A R Ax x Rys.9b - 11 - Sprawdzenie z warunku że suma momentów sił względem punktu B równa się zero (rys.9c)
y
(…)
… A o chropowatą poziomą płaszczyznę, a w punkcie C o gładki występ (rys.10). W położeniu równowagi belka tworzy z płaszczyzną poziomą kąt ϕ, a odcinek AC = 1,5l. Znaleźć współczynnik tarcia ślizgowego statycznego μ w punkcie A. l/2
l/2 B
l C
ϕ G
A Rys.10
Rozwiązanie - 12 - Siły działające na belkę (rys.10a)
+ϕN2 = 900
N2
y
rN2 C rN2 = AC= 1,5l, rG = AD = l
D N1 rG -ϕG = -(900 + ϕ)
G
ϕ
A
x Rys.10a
T1 rT1 = 0, rN1 = 0
(c)
Na rysunku 10b przedstawiono kąty między osią x i wektorami sił
αN2 = 900 + ϕ
N2
y
αG
N1 αN1 αG = 2700
G
ϕ
A x
Rys.10b
T1 αT1 = 00, αN1 = 900
, , (d)
(e)
Po podstawieniu (c) i (d) do (e) otrzymujemy - 13 -
stąd
dla ϕ = 220 Zadanie 11
Ciało o masie m zostało zawieszone na końcu liny nawiniętej na bęben o promieniu r, mogącym obracać się bez tarcia wokół poziomej osi. Bęben ten jest sztywno…
... zobacz całą notatkę






Komentarze użytkowników (0)