To tylko jedna z 5 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


Ćwiczenie 9 - 32 -
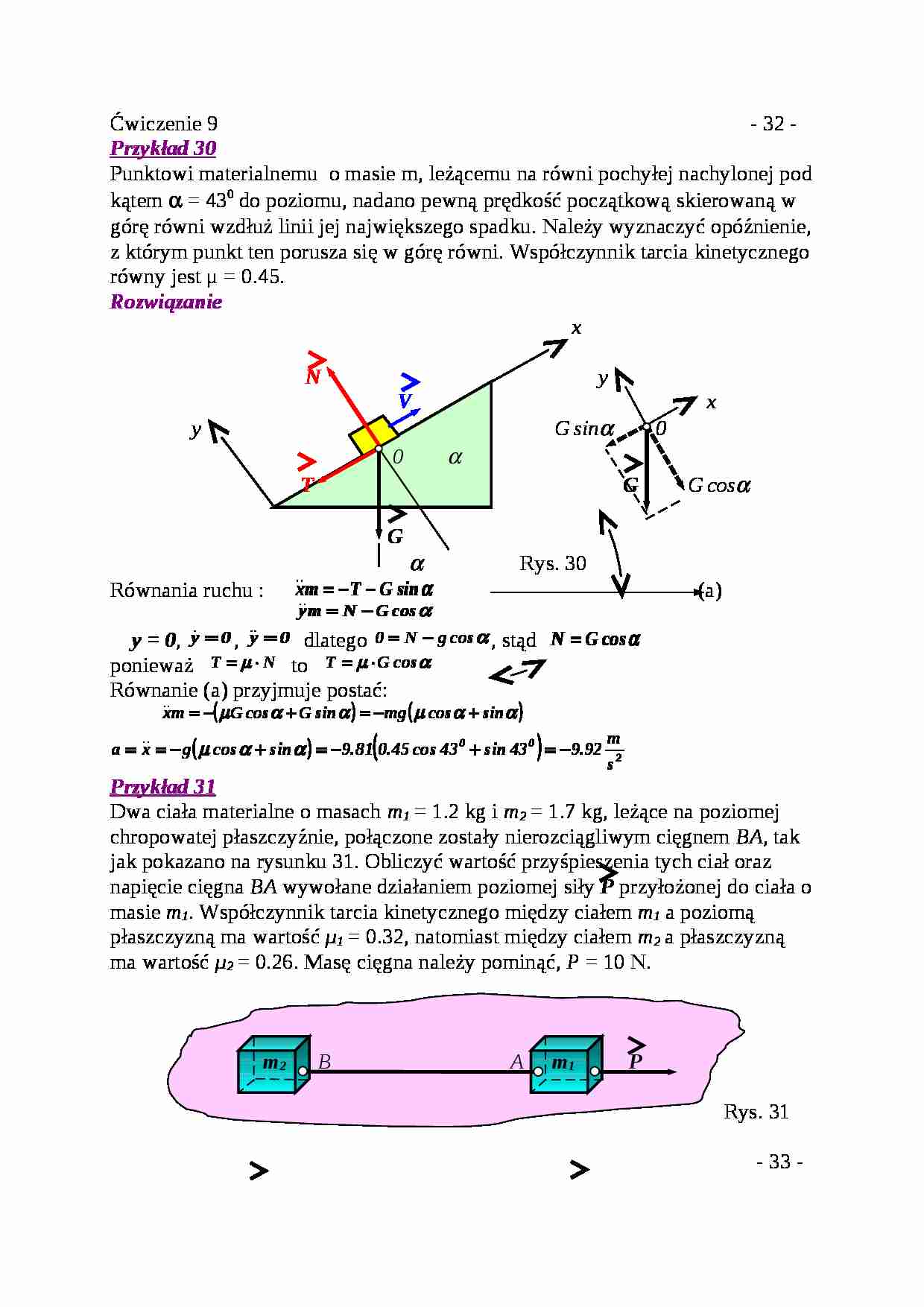
Przykład 30 Punktowi materialnemu o masie m, leżącemu na równi pochyłej nachylonej pod kątem α = 43 0 do poziomu, nadano pewną prędkość początkową skierowaną w górę równi wzdłuż linii jej największego spadku. Należy wyznaczyć opóźnienie, z którym punkt ten porusza się w górę równi. Współczynnik tarcia kinetycznego równy jest μ = 0.45.
Rozwiązanie x N y V x y G sin α 0 0 α T G G cos α G α Rys. 30
Równania ruchu : (a)
y = 0 , , dlatego , stąd ponieważ to Równanie (a) przyjmuje postać:
Przykład 31 Dwa ciała materialne o masach m 1 = 1.2 kg i m 2 = 1.7 kg, leżące na poziomej chropowatej płaszczyźnie, połączone zostały nierozciągliwym cięgnem BA , tak jak pokazano na rysunku 31. Obliczyć wartość przyśpieszenia tych ciał oraz napięcie cięgna BA wywołane działaniem poziomej siły P przyłożonej do ciała o masie m 1 . Współczynnik tarcia kinetycznego między ciałem m 1 a poziomą płaszczyzną ma wartość μ 1 = 0.32, natomiast między ciałem m 2 a płaszczyzną ma wartość μ 2 = 0.26. Masę cięgna należy pominąć, P = 10 N.
m 2 B A m 1 P Rys. 31
- 33 -
N 2 N 1 y m 2 S 2 - S 2 B A -S 1 S 1 m 1 P x
(…)
… którego masy nie uwzględniamy (b)
Siły działające na masę 2
, , , (c)
Ponieważ pręt BA porusza się ruchem postępowym to , stąd (d)
Z równania (b) Z równania (c) (e)
Z warunku (d) Z równania (e) Przykład 32 - 34 -
Pod jakim kątem należy wystrzelić pocisk o masie m, aby osiągnąć maksymalny zasięg strzału L, przy znanej prędkości początkowej pocisku V0. Określić również wartości maksymalnego zasięgu L…
... zobacz całą notatkę






Komentarze użytkowników (0)