To tylko jedna z 18 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę


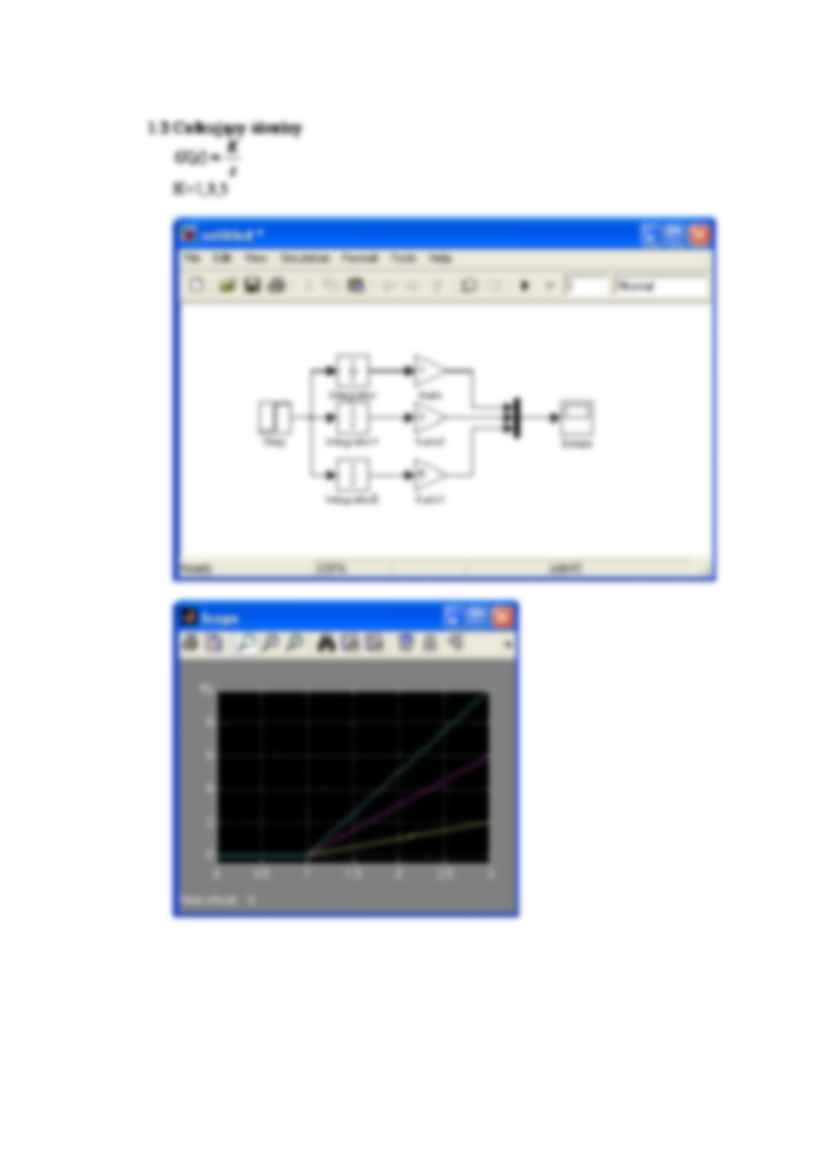
Zajęcia V Wyznaczanie charakterystyk skokowych podstawowych elementów dynamicznych. Cel ćwiczenia: zapoznanie studentów z charakterystykami skokowymi podstawowych elementów dynamicznych oraz określenie wpływu poszczególnych parametrów na kształt charakterystyk. Wstęp: Odpowiedź skokowa jest odpowiedzią y(t) układu dynamicznego na wymuszenie x(t) przyjmujące postać skoku jednostkowego 1(t) . Liniowe elementy dynamiczne opisywane są za pomocą transmisjii operatorowej K(s) definiowanej jako stosunek trasformat Laplace’a sygnału wyjściowego y(t) oraz sygnału wejściowego x(t) (przy zerowych warunkach początkowych): ) ( ) ( ) ( s X s Y s G = Charakterystyki skokowe można wyznaczyć: • analitycznie transformata Laplace’a skoku jednostkowego wynosi: s t t x L s X / 1 )] ( 1 ) ( [ ) ( = = = obliczając odwrotną transformatę Laplace’a: ⎥⎦ ⎤ ⎢⎣ ⎡ = − ) ( 1 ) ( 1 s K s L t y uzyskujemy odpowiedź układu na skok jednostkowy, • eksperymentalnie na podstawie zarejestrowanej eksperymentalnie odpowiedzi skokowej można określić rodzaj elementu oraz oszacować wartość parametrów transmitancji. Przebieg zajęć: 1. W środowisku MATLAB-SIMULINK przygotować odpowiednie schematy złożone ze źródła wymuszenia (skok jednostkowy), obiektu i oscyloskopu. Przeprowadzić symulacje i określić wpływ parametrów transmitancji na uzyskane charakterystyki. Jako obiekty można wybrać: 1.1 Obiekt proporcjonalny G(s)=K K=1,2,3 1.2 Całkujący idealny s K s G = ) ( K=1,3,5 1.3 Całkujący rzeczywisty ) 1 ( ) ( + = Ts s K s G K=1, 2 T=0.1 K=1 T=0.1, 2 1.4 Różniczkujący idealny Ks s G = ) ( K=0.1,5 1.5 Różniczkujący rzeczywisty 1 ) ( + = Ts Ks s G K=0.1 T=0.1, 0.5 K=2 T=0.1, 0.5 1.6 Inercyjny pierwszego rzędu 1 ) ( + = Ts K s G K=1, 3 T=1 K=1 T=0.1, 4 1.7 Oscylacyjny drugiego rzędu 1 2 ) ( = K s
... zobacz całą notatkę






Komentarze użytkowników (0)