Całki potrójne

Notatka składa się z 5 stron a jej zawartość jest następująca: definicja całki potrójnej, interpretacja geometryczna i fizyczna całki potrójnej, własności całki potrójnej, twierdzenie całkowe o wartości średniej, twierdzenie o zamianie całki potrójnej na całkę iterowaną, definicja obszaru normalnego, całka potrójna po obszarze normalnym, wyprowadzenie wzoru na całkę potrójną w obszarze normalnym, materiał zawiera również rysunki na których jest zaznaczone jak można interpretować całkę potrójną
                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                        

(…)

… CAŁKI POTRÓJNE
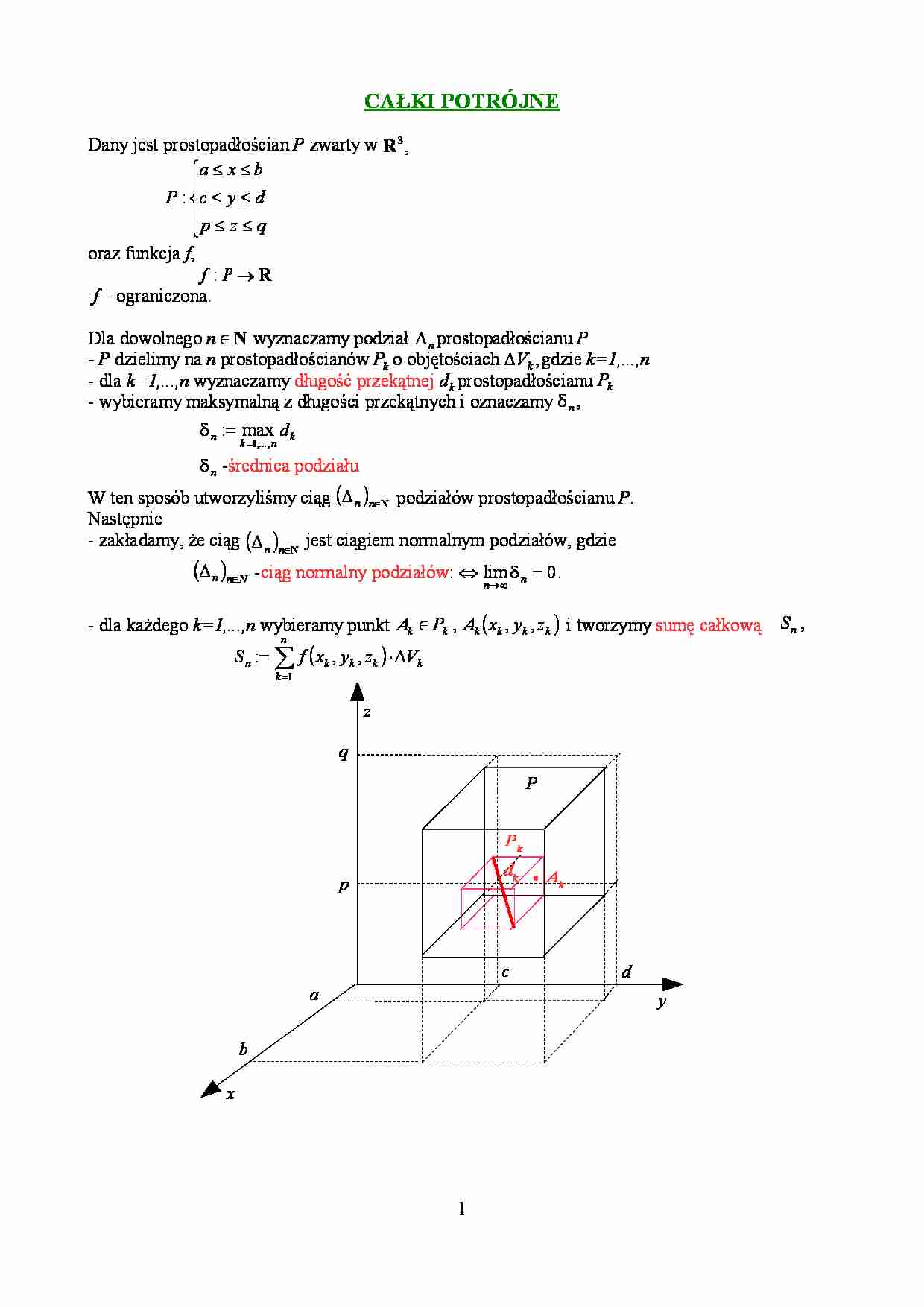
Dany jest prostopadłościan P zwarty w R 3 ,
a  x  b

P : c  y  d
p  z  q

oraz funkcja f,
f :PR
f – ograniczona.
Dla dowolnego n  N wyznaczamy podział  n prostopadłościanu P
- P dzielimy na n prostopadłościanów Pk o objętościach Vk , gdzie k=1,...,n
- dla k=1,...,n wyznaczamy długość przekątnej d k prostopadłościanu Pk
- wybieramy maksymalną z długości przekątnych i oznaczamy  n ,
 n : max d k
k 1,..., n
 n -średnica podziału
W ten sposób utworzyliśmy ciąg  n nN podziałów prostopadłościanu P.
Następnie
- zakładamy, że ciąg  n nN jest ciągiem normalnym podziałów, gdzie
 n nN
-ciąg normalny podziałów:  lim  n  0 .
n
- dla każdego k=1,...,n wybieramy punkt Ak  Pk , Ak  xk , yk , z k  i tworzymy sumę całkową
n
S n :  f xk , yk , z k   Vk
k 1
z
q
P
Pk
dk
p
c
a
Ak
d
y
b
x
1
Sn ,
Definicja (całki potrójnej)
Jeśli dla każdego normalnego ciągu podziałów prostopadłościanu P, ciąg sum cząstkowych S n nN
jest zbieżny do tej samej granicy właściwej, niezależnej od wyboru punktów Ak , to tę granicę
nazywamy całką potrójną funkcji f w prostopadłościanie P i oznaczamy  f x, y , z dV ,
 f x, y, z dV : lim S n .
P
 n 0
P
Uwaga
Jeśli funkcja ograniczona f jest ciągła poza zbiorem miary zero (zbiór miary zero w R3 to taki zbiór,
który można pokryć skończoną liczbą prostopadłościanów, których suma objętości jest dowolnie
mała (czyli mniejsza niż ε )), to funkcja f jest całkowalna w prostopadłościanie P.
Interpretacja geometryczna
f  x, y, z   1   dV  VP - objętość prostopadłościanu P.
P
Interpetacja fizyczna
1.   x, y, z - gęstość objętościowa masy prostopadłościanu P 
   x, y, z dV - masa prostopadłościanu P.
P
2.   x, y, z - gęstość objętościowa ładunku elektrycznego prostopadłościanu P 
    x, y, z dV - całkowity ładunek elektryczny zgromadzony w P.
P
Własności całki potrójnej
Całka potrójna ma własności analogiczne jak całka podwójna (liniowość, addywność,
ograniczoność).
Twierdzenie (całkowe…
... zobacz całą notatkę