1
Bilansowanie zasobów wodnych
Definicje:
1. Zasoby wodne są to wszelkie wody znajdujące się na danym obszarze stale lub występujące na nim czasowo (Dębski).
2. Przepływ średni roczny – Qśr -jest to średnia arytmetyczna przepływów z wielolecia.
3. Średni roczny odpływ - Vśr średnia arytmetyczna z odpływów rocznych z wielolecia. Jest to
całkowita ilość wody w mln m3 jaka przeciętnie w ciągu całego roku przepływa przez profil
ujściowy, pojęta jako średnia arytmetyczna z wielolecia (Lambor).
4. Moduł odpływu - dzieląc średni roczny odpływ przez powierzchnię zlewni otrzymamy tzw.
moduł odpływu MO.
5. Moduł opadu - odpowiada średniemu rocznemu opadowi z wielolecia MP. Jest to normalny opad roczny wyrażony w mm.
6. Współczynnik odpływu α - jest to liczba niemianowana, mniejsza od jedności. Wielkość ta
charakteryzuje potencjał zlewni i po pomnożeniu jej przez 100 charakteryzuje procentowy
udział odpływu w stosunku do opadu.
α=
MO
MP
2
Jednym ze sposobów opracowania bilansu wodnego jest porównanie ilości wody jaka
dostaje się do zlewni z wodą zatrzymaną w zlewni oraz ilością jaka z niej odpływa w danym
przedziale czasu (np miesiąc, rok, wielolecie).
Ponieważ rozwój przemysłu, różnego rodzaju zjawiska klimatyczne (ciąg lat suchych,
mokrych), wymuszają zmiany w zasobach wodnych i sposobach użytkowania wody zmieniają
się również składniki bilansu. Stąd konieczność sporządzania różnego rodzaju bilansów. Wybór sposobu rozwiązania zależy od rozpatrywanego okresu czasu, od wielkości bilansowanego obszaru, od celu jakiemu ma służyć bilans itp. Wymaga on dokładnego rozpoznania terenu, jego budowy geologicznej, pokrycia, ukształtowania, źródeł zasilania itp.
Bilanse szczegółowe, które oprócz opadu, odpływu i strat na parowanie uwzględniają
również retencję opracowuje się głownie dla małych obszarów i dla krótkich okresów czasu.
Dla długich okresów i znacznie większych obszarów wprowadza się uogólnienia pozwalające na uzyskanie wyników, charakterystycznych dla wielolecia. Mamy wówczas do
czynienia z bilansami surowymi polegającymi na zestawieniu opadu i odpływu.
3
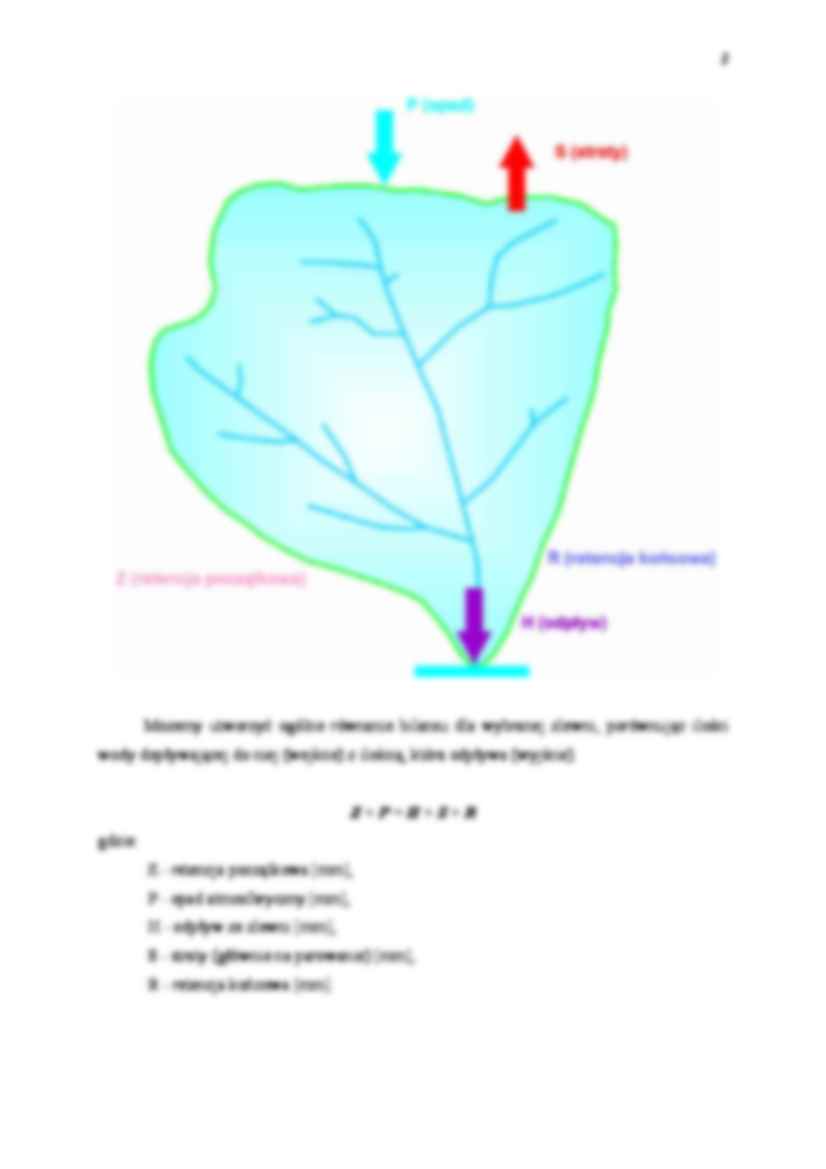
Możemy utworzyć ogólne równanie bilansu dla wybranej zlewni, porównując ilości
wody dopływającej do niej (wejście) z ilością, która odpływa (wyjście).
Z+P=H+S+R
gdzie:
Z - retencja początkowa [mm],
P - opad atmosferyczny [mm],
H - odpływ ze zlewni [mm],
S - straty (głównie na parowanie) [mm],
R - retencja końcowa [mm].
4
Przekształcając kolejno, otrzymujemy:
Z−R=H +S−P
R − Z = P − (H + S)
R − Z = ∆R
∆R = P − H − S
Wielkość ∆R może być ujemna lub dodatnia. Możemy wówczas napisać:
P = H + S ± ∆R
W przypadku, kiedy ∆R równa się zero mówimy o uproszczonym bilansie wodnym zlewni.
P= H+S
Dzieląc równanie bilansu przez opad otrzymamy:
H S
+ =1
P P
Oznaczając: S/P = β otrzymamy zależność współczynnika odpływu α od parametru β współczynnika strat. Możemy napisać:
α = 1− β
Uproszczony bilans wodny stosujemy często w przypadku kiedy rozpatrujemy dłuższy okres,
np wielolecie. Zdarza się bowiem, że
(…)
… - opad normalny roczny [m],
A - powierzchnia zlewni [km2],
Cs - współczynnik odpływu - wartość stabelaryzowana
0,03171 - zamiennik wartości wskaźnika opadu wyrażonego w m na przepływ [m3/s].
Wartości współczynnika do wzoru Iszkowskiego
Grupa topograficzna zlewni
Współczynnik odpływu Cs
Bagna i niziny
0,20
Niziny i płaskie wysoczyzny
0,25
Częściowo niziny, częściowo pagórki
0,30
Pagórki o łagodnych stokach
0,35
Częściowo przedgórza, częściowo pagórki lub strome pagórki
0,40
Karkonosze, Sudety, Beskidy (średnie)
0,55
Wysokie góry
0,6 - 0,7
7
Kajetanowicz współczynnik odpływu określa następująco:
α g = 0.095 * Ws0.2 * Ψ 0.084
α n = 0.063 * Ws0.25 * Ψ 0.1
gdzie:
αg - współczynnik odpływu dla rzek górskich,
αn - współczynnik odpływu dla rzek nizinnych,
Ws - średnia wysokość nadmorska zlewni liczona wg…
... zobacz całą notatkę





Komentarze użytkowników (0)