To tylko jedna z 3 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
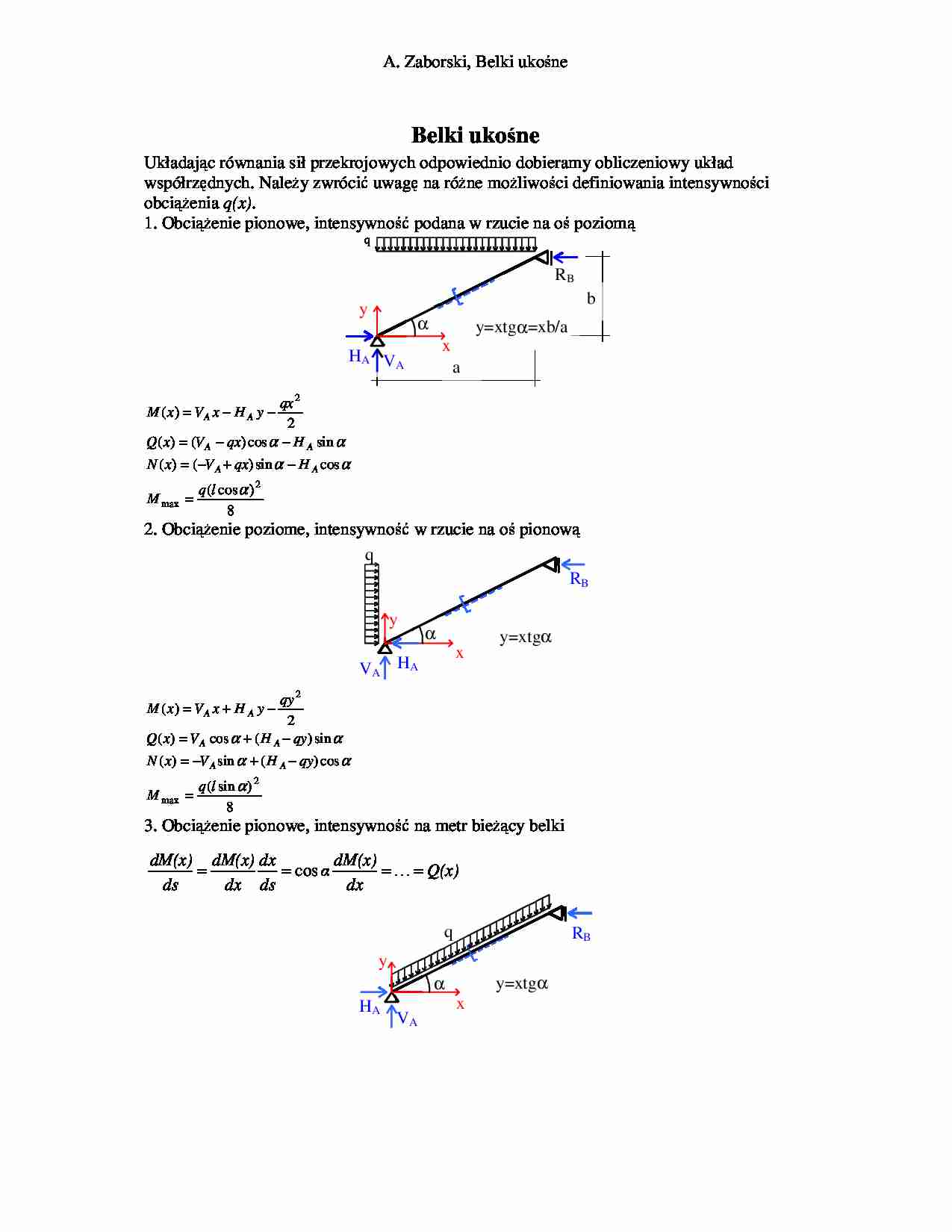


A. Zaborski, Belki uko ne Belki uko ne Układaj c równania sił przekrojowych odpowiednio dobieramy obliczeniowy układ współrz dnych. Nale y zwróci uwag na ró ne mo liwo ci definiowania intensywno ci obci enia q(x) . 1. Obci enie pionowe, intensywno podana w rzucie na o poziom a b α HA VA x y RB q y=xtg α=xb/a 8 ) cos ( cos sin ) ( ) ( sin cos ) ( ) ( 2 ) ( 2 max 2 α α α α α l q M H qx V x N H qx V x Q qx y H x V x M A A A A A A = − + − = − − = − − = 2. Obci enie poziome, intensywno w rzucie na o pionow α q x y RB HA VA y=xtg α 8 ) sin ( cos ) ( sin ) ( sin ) ( cos ) ( 2 ) ( 2 max 2 α α α α α l q M qy H V x N qy H V x Q qy y H x V x M A A A A A A = − + − = − + = − + = 3. Obci enie pionowe, intensywno na metr bie cy belki α x y q RB HA VA y=xtg α Q(x) dx dM(x) ds dx dx dM(x) ds dM(x) = = = = cos A. Zaborski, Belki uko ne dx x dM ds dx dx x dM ds s dM qx H V x N qx H V x Q x x q y H x V x M A A A A A A ) ( cos ) ( ) ( sin cos cos sin ) ( cos cos sin cos ) ( 2 cos ) ( α α α α α α α α α α = = + − − = − + = − − = Zadanie, po odpowiednim przeliczeniu intensywno ci obci enia ci głego (z warunku równo ci wypadkowych), mo na oblicza jak w przykładzie 1. Obliczenia w układzie współrz dnych zwi zanym z osi belki s mniej wygodne: α x q RB VA HA 8 ) cos ( sin ) ( cos ) ( 2 cos ) ( max α α α α l ql M qx H x N qx V x Q x qx x V x M A A A = + − = − = − = 4. Obci enie prostopadle do osi belki, intensywno obci enia podana na metr bie cy belki x α q RB VA HA 8 ) ( ) ( 2 ) ( 2 max 2 ql M H x N qx V x Q qx x V x M A A A = − = − = − = W „normalnym” układzie współrz dnych, niezwi zanym z osi belki: y x α q RB VA HA moment zginaj cy zapisze si : 2 cos 2 cos 2 cos ) ( − − = − − = α α α x q y H x V x x q y H x V x M A A A
... zobacz całą notatkę






Komentarze użytkowników (0)