To tylko jedna z 8 stron tej notatki. Zaloguj się aby zobaczyć ten dokument.
Zobacz
całą notatkę
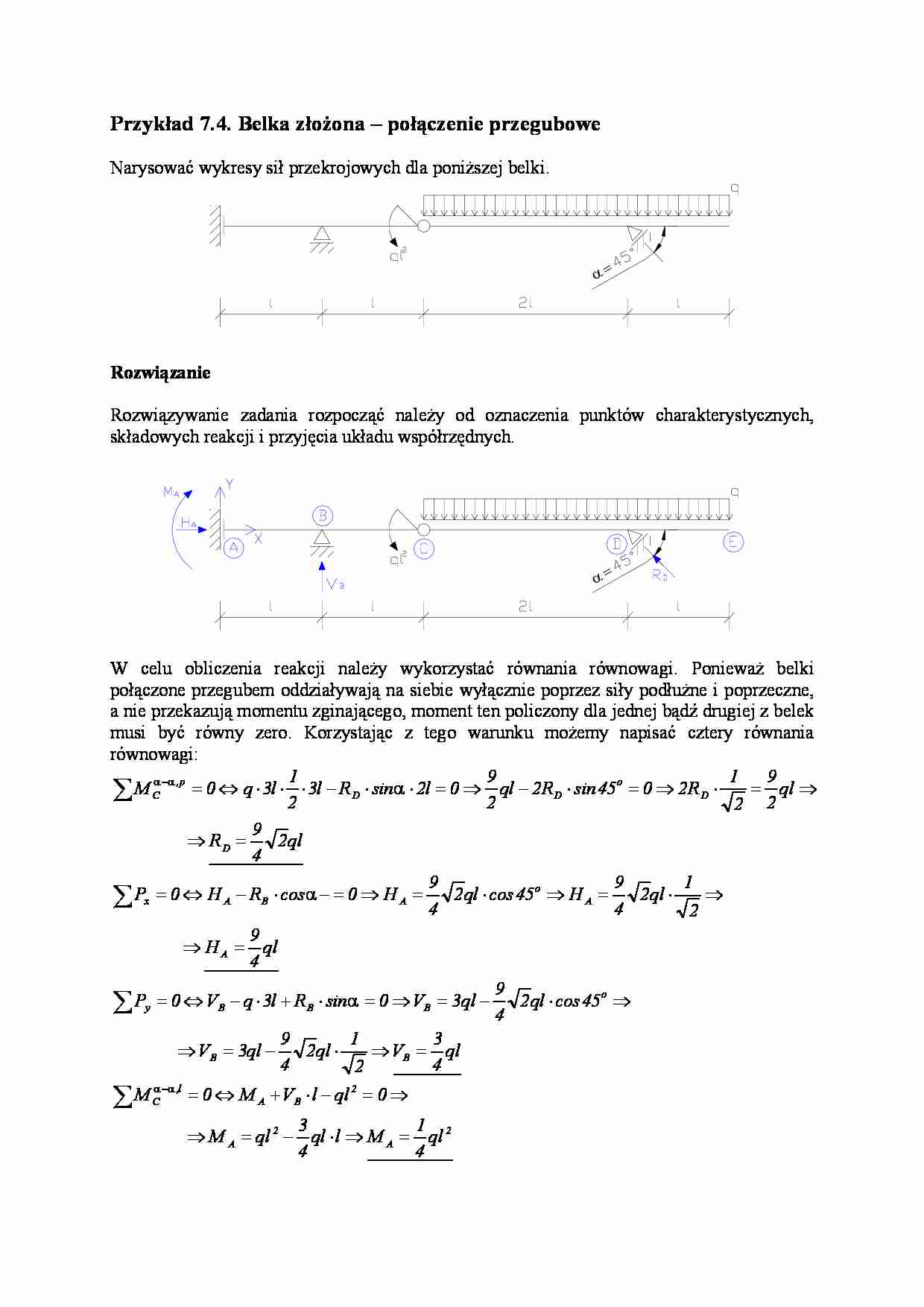


Przykład 7.4. Belka złożona – połączenie przegubowe Narysować wykresy sił przekrojowych dla poniższej belki. α = Rozwiązanie Rozwiązywanie zadania rozpocząć należy od oznaczenia punktów charakterystycznych, składowych reakcji i przyjęcia układu współrzędnych. α = W celu obliczenia reakcji należy wykorzystać równania równowagi. Ponieważ belki połączone przegubem oddziaływają na siebie wyłącznie poprzez siły podłużne i poprzeczne, a nie przekazują momentu zginającego, moment ten policzony dla jednej bądź drugiej z belek musi być równy zero. Korzystając z tego warunku możemy napisać cztery równania równowagi: 2 2 2 4 1 4 3 0 0 4 3 2 1 2 4 9 3 45 2 4 9 3 0 3 0 4 9 2 1 2 4 9 45 2 4 9 0 0 2 4 9 2 9 2 1 2 0 45 2 2 9 0 2 3 2 1 3 0 ql M l ql ql M ql l V M M ql V ql ql V cos ql ql V sin R l q V P ql H ql H cos ql H cos R H P ql R ql R sin R ql l sin R l l q M A A B A l, C B B o B B B y A A o A B A x D D o D D p , C = ⇒ ⋅ − = ⇒ ⇒ = − ⋅ + ⇔ = = ⇒ ⋅ − = ⇒ ⇒ ⋅ − = ⇒ = ⋅ + ⋅ − ⇔ = = ⇒ ⇒ ⋅ = ⇒ ⋅ = ⇒ = − ⋅ − ⇔ = = ⇒ ⇒ = ⋅ ⇒ = ⋅ − ⇒ = ⋅ ⋅ − ⋅ ⋅ ⋅ ⇔ = ∑ ∑ ∑ ∑ − − α α α α α α α Tak więc √ α = Obecnie możemy już przystąpić do rysowania wykresów sił przekrojowych. Wykres siły normalnej N Jak widać jedynym obciążeniem podłużnym działającym na rozpatrywaną belkę są siły skupione - reakcje podpór działające w punktach A i D. Wynika z tego, że na wykresie N w punktach tych musi pojawić się skok wartości funkcji N(x) , natomiast pomiędzy nimi wykres musi być stały. Kierunek działania reakcji – „do belki” – oznacza ujemny znak siły N . Poza odcinkiem A-D, tj. na odcinku D-E siła N=0 . Wykres siły tnącej T Rysowanie ponownie zaczynamy w punkcie A, przesuwać się będziemy w prawo. Ponieważ na odcinku A-B nie występują siły działające prostopadle do belek, więc N=0 . 2 W punkcie B przyłożona jest siła ql 4 3 wywołująca obrót rozważanej (lewej) części układu zgodny z kierunkiem ruchu wskazówek zegara, co oznacza, że siła T zwiększa się skokowo w tym punkcie o
... zobacz całą notatkę






Komentarze użytkowników (0)